UFSC – Lista 1.6 - Continuidade: mais propriedades e Teorema do Valor Intermediário – C2
C2. Classifique cada item abaixo como verdadeiro ou falso.
a) Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo .
b) Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo .
c) Seja . Pelo Teorema do Valor Intermediário, é possível concluir que existe ∈ [0,4] tal que .
d) A função possui, pelo menos, uma raiz real.
e) Toda função contínua possui, pelo menos, uma raiz real.
Passo 1
Faaala galerinha, vamo provar cada item que ela pede de uma maneira bem detalhada, podem ficar tranquilos. Começando pelo item (a):
Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo
Show, bora lá! Podemos observar que a função não é contínua nesse intervalo, visto que, aplicando um valor intermediário na função (valor intermediário entre o intervalo é ), temos:
Ou seja, uma indeterminação. Dessa forma, não podemos afirmar nada e a alternativa é falsa.
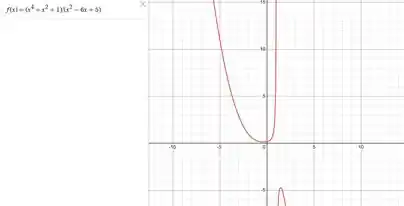
Saca só essa imagem, nela podemos perceber que temos uma raiz real sim no intervalo.
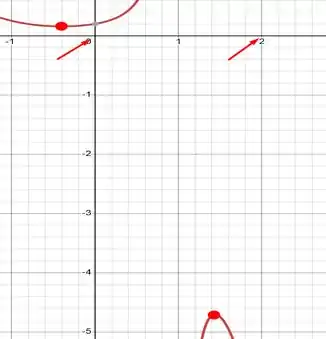
Na imagem, percebemos uma raiz real (representados pelos pontos vermelhos) dentro do intervalo (indicado pelas setas). Porém, pelo TVI, realmente não temos raiz real no intervalopodemos afirmar se há, ou não, raiz real nesse intervalo., Pportanto, o item é falso!
Passo 2
Vamo pro item (b)!
Agora, temos uma função dada por:
E queremos mostrar que, pelo TVI, é possível afirmar que possui pelo menos uma raiz real no intervalo Pelo Teorema do Valor Intermediário, é possível concluir que a função possui pelo menos uma raiz real no intervalo .
Tá bem, vamo lá. Primeiro temos alguns fatos nesse argumento do item. Primeiro que de fato, a função é contínua no intervalo e em todo o conjunto dos reais. Agora vamos estudar a função nos valores extremos do intervalo: Aplicando em e :
De fato, nesse intervalo a nossa função contínua passa por valores positivos e negativos, portanto podemos afirmar pelo TVI que ela possui raiz real; ou seja, passou por zero ao menos uma vez. Logo, o nosso item é verdadeiro!
Passo 3
Vamo pro item (c)!
Seja . Pelo Teorema do Valor Intermediário, é possível concluir que existe ∈ [0,4] tal que .
De começo, temos que de fato, a função é contínua no intervalo e em todo o conjunto dos reais. Ela é tranquila de aplicar os intervalos. Mas caso ainda não seja tão tranquilo assim, a gente tem o seguinte:
Então, de fato, pelo TVI afirmamos que nesse intervalo a nossa função contínua passa pelo menos por valores de 3 a 9, portanto podemos afirmar que ela, em algum ponto , possui valor 7. Portanto, item verdadeiro!
Passo 4
Simbora pro item (d)!
A função possui, pelo menos, uma raiz real.
Resposta:
Show, aplicando os valores a gente prova que o intervalo dela é real (e tem umas raízes bem loucas, jaja mostro pra vocês).
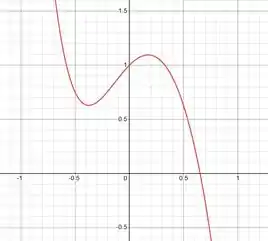
Estudemos seus valores nos extremos de um intervalo [0,1] pra gente observaranalisarmos como ela se comporta passando pelo 0. Porque, se para um dos extremos ela for positiva, e para o outro for negativa ela for real nesses pontos, a gente conclui que ela possui pelo menos alguma raiz real.
De fato, nesse intervalo a nossa função contínua passa por valores positivos e negativos, portanto podemos afirmar pelo TVI que ela possui raiz real; ou seja, passou por zero ao menos uma vez. Logo, item verdadeiro mais uma vez!
Passo 5
Pra finalizar, temos o item (e):
Toda função contínua possui, pelo menos, uma raiz real.
Ora, não necessariamente! Você consegue pensar em uma função que não tem raiz real? Eu conheço uma fácil! Basta tomarmos como exemplo, ela é contínua, mas não possui raiz.
Passo 6
Resposta
a) Falso
b) Verdadeiro
c) Verdadeiro
d) Verdadeiro
e) Falso