USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 1.14
Sejam o círculo de raio e centro em e , o círculo de raio , , e centro em . Sejam ainda o ponto e o ponto de intersecção dos círculos e situado no primeiro quadrante.
Se é a intersecção da reta com o eixo , o que acontecerá com , quando encolher arbitrariamente?
Passo 1
Fala aí pessoal, tudo bem?
Nessa questão precisamos utilizar uma ideia de limite mais geométrica mesmo.
Temos dois círculos:
centrado em e com raio igual a .
: centrado em e com raio igual a . Onde
No círculo , o seu ponto de intersecção com o eixo , chamamos de .
E, o ponto de intersecção de com , no primeiro quadrante chamamos de . Daí, traçamos uma reta ligando os pontos e , e observamos a sua intersecção com o eixo . Esse ponto é justamente o ponto .
O enunciado nos pede para dizer qual será o ponto quando o raio da circunferência começa a diminuir indefinidamente.
É como se quiséssemos saber o limite de quando .
Sacaram?
Pra fazer isso vamos desenhar a situação geométrica e analisar o que acontece no limite.
Vamo nessa!
Passo 2
Bom, vamos começar desenhando o círculo
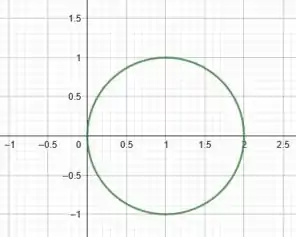
Agora vamos desenhar o círculo , que está centrado em . Vamos considerar um raio genérico entre e .
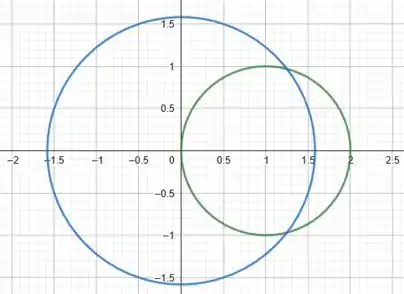
Agora, ligando os pontos e , temos:
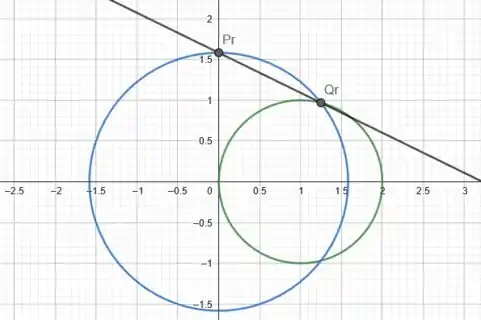
Encontramos bem na intersecção da reta traçada com o eixo .
Excelente!
Passo 3
Agora que já desenhamos a situação, vamos pensar um pouquinhio...
Se o raio passar a diminuir indefinidamente, a nossa circunferência vai se reduzir a um ponto, bem no centro dela. Ou seja, a circunferência se reduzirá ao ponto .
Consequentemente, o ponto passará a valer .
E, a intersecção das circunferências também estará bem no ponto
Ou seja, teremos:
Logoo, também se reduzirá a um ponto. E, adivinha qual é?
Isso mesmo:
Prontinho pessoal! Essa é a respota.
Obrigado pela atenção de todos 😊