Considere definida por
- Determine os pontos críticos de .
- Em quais intervalos é crescente?
- Em quais intervalos é decrescente
- Determine, se houver, os pontos de mínimo local de .
- Determine, se houver, os pontos de máximo local de .
- Em quais intervalos, se houver, o gráfico de é côncavo para cima?
- Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
- Determine, se houver, os pontos de inflexão do gráfico de .
- Calcule e
- Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Passo 1
Vamos começar pelos pontos críticos, para isso devemos achar a derivada de
Vamos igualar essa derivada a
Isso nos diz que
E temos um ponto crítico.
Passo 2
Vamos analisar o sinal da derivada, para isso vamos primeiro dar uma arrumadinha nela
E o sinal vai depender só do numerador, isso porque é sempre positivo. Para ser crescente devemos ter essa derivada sendo positiva, então
Isso implica que
E a função vai ser crescente quando for positivo.
Passo 3
Como já vimos a derivada depende só do numerador daquela expressão que achamos, então para a função ser decrescente devemos ter a derivada sendo negativa, então
Isso implica que
E a função vai ser decrescente quando for negativo.
Passo 4
Temos um ponto crítico, nele é onde temos troca de sinal da derivada indo de para , ou seja, pelo teste da primeira derivada esse ponto vai ser de mínimo local, vamos achar o valor de desse ponto
E o ponto é um ponto de mínimo
Passo 5
Como só temos um ponto crítico e esse ponto é de mínimo não vamos ter ponto de máximo local, outra forma de ver isso seria repara que a derivada nunca troca de positivo para negativo, que é onde acontece os pontos de máximo locais.
Passo 6
Para olharmos a concavidade devemos achar a segunda derivada
E vamos ter
Sempre, isso nos diz que a soma também vai ser sempre positiva, então
Sempre! Isso nos diz que o gráfico vai ser côncavo para cima em todos os reais
Passo 7
Como vimos no passo anterior, o gráfico vai ser côncavo para cima em todos os reais, isso nos diz que ele nunca vai ser côncavo para baixo.
Passo 8
Como não temos troca de concavidade não vamos ter pontos de inflexão
Passo 9
Vamos agora achar esses limites que ele pediu
Passo 10
O gráfico vai ficar algo parecido com uma parábola, só que um ponto mais “gordinho”, como só temos um máximo e não temos nenhuma assíntota não precisamos das linhas auxiliares para esse gráfico.
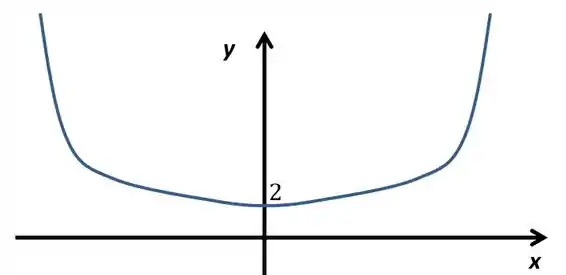
Resposta
- Não tem
- Todo o gráfico
- Não tem
- Não tem