Considere a função:
(i) Encontre o domínio de .
(ii) Caso existam, determine as assíntotas horizontais e verticais de .
(iii) Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo locais e globais e os seus valores.
(iv) Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
(v) Encontre os pontos de interseção do gráfico de com os eixos e esboce o gráfico de usando as informações obtidas nos itens anteriores.
Passo 1
Vamos ver aqui as restrições ao domínio de . Como o ln não pode ter argumento negativo ou zero, precisamos que:
Da mesma maneira, não podemos ter divisão por zero na fração, e:
Que já está incluso na restrição anterior. Assim sendo:
Ou seja, o conjunto dos números reais positivos. Você também poderia escrever:
Passo 2
As assíntotas horizontais são testadas para tendendo a mais e menos infinito. Não incluiremos o segundo, pois não faz parte do domínio. Assim sendo:
Ou seja, a função não tem assíntota horizontal.
As assíntotas verticais ocorrem nos pontos de indeterminação ou singularidade, o que ocorre em . Testando para esse ponto:
Vamos tentar juntar tudo num mesmo denominador para tentar sair dessa indeterminação:
Aplicando L’Hôpital:
Portanto, temos uma assíntota vertical em .
Passo 3
A função cresce quando a derivada é positiva e decresce quando a derivada é negativa. Vamos derivar então para saber quando isso acontece:
O denominador está elevado ao quadrado e não influenciará no sinal da derivada, que será determinado pelo numerador, positivo para e negativo para .
Dessa maneira, a função é crescente para:
E decrescente para:
E tem pontos críticos em , onde a derivada não existe, e em , onde zera. A partir dos dados obtidos e do teste da primeira derivada, concluímos também que é um ponto de mínimo, uma vez que a derivada é negativa à esquerda e positiva à direita desse ponto.
Como temos uma assíntota tendendo a mais infinito na fronteira esquerda do domínio da função, em , e a função tende a mais infinito quando , todos os demais valores possíveis para são maiores que este mínimo e, portanto, trata-se de um mínimo global.
Passo 4
A função é côncava para cima quando a segunda derivada é positiva e côncava para baixo quando negativa. Dessa maneira, vamos calcular a segunda derivada para saber.
Vamos fazer um quadro de sinais para determinar o sinal da segunda derivada:

A partir do sinal de cada expressão:

Desconsiderando a parcela negativa, que não faz parte do domínio da função, concluímos que a função é côncava para cima para:
E côncava para baixo para:
Passo 5
A função não intercepta os eixos, pois o domínio está à direita da origem e o mínimo global é positivo. Dessa maneira, a partir dos dados obtidos, chegamos ao gráfico:
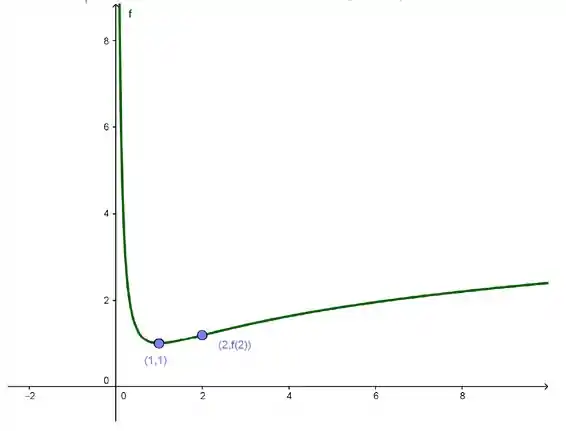
Resposta
Ei, a resposta está no passo a passo :)