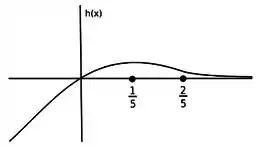
Para a função dada por:
a) Determine os intervalos de crescimento e decrescimento.
b)Faça o estudo da concavidade.
c) Determine as assíntotas horizontais.
b) Esboce o gráfico.
Passo 1
a) Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de . Então vamos começar derivando a função:
Passo 2
Agora podemos estudar o sinal da derivada. Observe que para qualquer . Então o sinal da derivada depende apenas da reta . Vamos analisar o sinal dela:
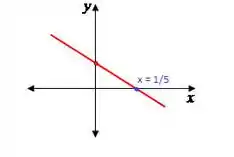
A reta é positiva antes de e negativa depois desse ponto. Assim:
- Intervalo de crescimento de :
- Intervalo de decrescimento de :
Passo 3
b) Temos que descobrir onde a função é côncava pra cima ou côncava pra baixo. Como fazer isso? Analisando o sinal da segunda derivada. Então vamos derivar :
Passo 4
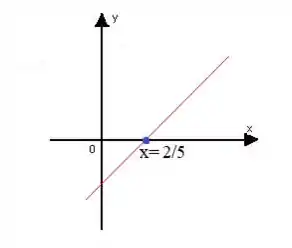
Assim como no item (a), o sinal não vai depender de , apenas da reta cujo gráfico está esboçado abaixo:
Então:
- quando
- quando
Portanto a concavidade de é voltada pra cima se e voltada pra baixo se
Passo 5
c) Pra calcular as assíntotas horizontais temos que fazer os limites com . Vamos lá:
Aplicando L’Hospital:
Passo 6
Agora vamos fazer com
Portanto, só tem uma assíntota horizontal, que é
Passo 7
d) A partir das informações que obtivemos nos itens anteriores, o gráfico de fica assim:
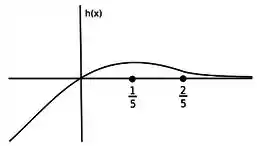
Resposta
a) Intervalo de crescimento de :
Intervalo de decrescimento de :
b) a concavidade de é voltada pra cima se e voltada pra baixo se
c)
d)