Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico

Ver Teoria
Exercício 831234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818284858687888990919293949596979899100

Enunciado

Considere a função g definida por

g x = x 2 - 4 2 x - 4

a) Determine o domínio da função g .

b) Determine os intervalos de crescimento e os de decrescimento de g , caso existam.

c) Determine as equações das retas assíntotas horizontais e verticais do gráfico de g , caso existam.

d) Utilizando as informações obtidas nos itens anteriores, esboce o gráfico de g e suas retas assíntotas, caso existam.

Passo 1

a) Temos duas restrições para o domínio:

x 2 - 4 ≥ 0

E

2 x - 4   ≠ 0

Resolvendo a primeira:

x 2 - 4 ≥ 0

x 2 - 4 ≥ 0

x 2 ≥ 4

- 2 ≥ x ≤ 2

      ⇓

- ∞ ,   - 2 ] ∪ [ 2 ,   + ∞ )

E agora a segunda:

2 x - 4   ≠ 0

2 x ≠ 4

x ≠ 2

Unindo os resultados encontrados descobrimos que o domínio é:

- ∞ ,   - 2 ] ∪ ( 2 ,   + ∞ )

Passo 2

b) Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de g . Então vamos começar derivando a função:

g ' x = 2 x 2 x 2 - 4 2 x - 4 - 2 x 2 - 4 ( 2 x - 4 ) ² = x 2 x - 4 - 2 x 2 - 4 x 2 - 4 ( 2 x - 4 ) ² = - 4 x + 8 x 2 - 4 ( 2 x - 4 ) ²

Passo 3

x , pois é composto de uma raíz quadrada e uma potência par. Então o sinal da derivada depende apenas da reta - 4 x + 8 . Vamos analisar o sinal dela:

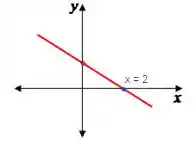
A reta é positiva (crescente) antes de x = 2 e negativa (decrescente) depois desse ponto, mas tome cuidado pois temos que considerar o domínio da função que é

- ∞ ,   - 2 ] ∪ ( 2 ,   + ∞ )

Portanto, a função não está definida em x = 2 . Antes desse ponto a função só está definida em - ∞ ,   - 2 ] e depois dele só está definida em 2 ,   + ∞ ) . Portanto:

  • Intervalo de crescimento de g : - ∞ ,   - 2 ]
  • Intervalo de decrescimento de g : 2 ,   + ∞ )

Passo 4

c) Pra calcular as assíntotas horizontais temos que fazer os limites com x → ± ∞ . Vamos lá:

lim x → + ∞ ⁡ x 2 - 4 2 x - 4 = lim x → + ∞ ⁡ x 2 x 2 - 4 x 2 2 x x - 4 x = lim x → + ∞ ⁡ 1 - 4 x 2 2 - 4 x = 1 - 0 2 - 0 = 1 2

Agora vamos fazer com x → - ∞

lim x → - ∞ ⁡ x 2 - 4 2 x - 4 = lim x → - ∞ ⁡ x 2 x 2 - 4 x 2 2 x - x - 4 ( - x ) = lim x → - ∞ ⁡ 1 - 4 x 2 - 2 - 4 ( - x ) = 1 - 0 - 2 - 0 = - 1 2

Portanto, g tem como assíntotas horizontais y = 1 2 e y = - 1 2

Passo 5

A partir do estudo do domínio, sabemos que o único x candidato à ser assíntota vertical é x = 2 , pois não pertence ao domínio. Teremos que calcular os limites laterais em torno desse ponto e se algum deles der ± ∞ então a reta x = 2 será assíntota vertical.

lim x → 2 + ⁡ x 2 - 4 2 x - 4 = lim x → 2 + ⁡ x - 2 ∙ x + 2 2 ( x - 2 ) = lim x → 2 + ⁡ x + 2 2 x - 2 = + ∞

Opa! Já deu infinito. Entao podemos afirmar que x = 2 é assíntota vertical.

Passo 6

d) Agora estamos prontos pra esboçar o gráfico, que fica assim:

Resposta

a) D o m g =   - ∞ ,   - 2 ] ∪ ( 2 ,   + ∞ )

b) Intervalo de crescimento de g : - ∞ ,   - 2 ] e Intervalo de decrescimento de g : 2 ,   + ∞ )

c) g tem como assíntotas horizontais y = 1 2 e y = - 1 2 e x = 2 como assíntota vertical.

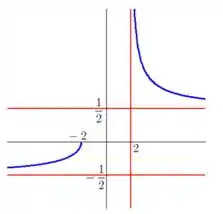d)

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2