Seja \ uma função com segunda derivada contínua e tal que:
- Determine . Qual o número de raízes que a função possui?
- Esboce, destacando todos os pontos relevantes, o gráfico de .
Passo 1
Basicamente essa é uma questão de esboço de gráfico em que (quase) todas as informações já foram dadas, e cabe a nós interpretá-las.
(a)
Antes do esboço, ele pediu o limite em e o número de raízes da função.
Vamos começar pelo limite. As informações que temos sobre a função em são:
E sabemos que
Portanto, para , é decrescente e côncava para baixo, então inevitavelmente teremos
Não está convencido? Pegue um pedaço de papel e desenhe uma curva decrescente e côncava para baixo!
Não tem como tender para um valor constante, fatalmente irá pra . Assim como uma curva crescente côncava pra cima tende para .
Passo 2
Agora vamos às raízes. O crucial aqui é selecionar as informações certas do monte que foi dado.
Vamos varrer o todo, de a e ver o que está acontecendo com essa função.
Lá em , temos
E temos que
Portanto, não temos nenhuma raiz de a . Aliás, foi dado .
Passo 3
Só que acontece que é crescente em .
Opa, então nesse intervalo pode ser que tenha uma raiz. Só uma porque se a função só cresce sem parar, não tem como ela cruzar o eixo mais de uma vez.
E de fato, no intervalo tem uma raiz, já que
Em tínhamos um valor negativo () e agora, nos aproximando de , a função explodiu pra , que é obviamente positivo.
Ok, então de a temos uma raiz.
Passo 4
Agora a informação importante é que é decrescente em . Ou seja, pode ser que tenha uma raiz no intervalo .
Mas peraí, a gente viu lá atrás que
A função que estava lá pra nas redondezas de depois decresce pra quando , então certamente temos uma raiz no intervalo .
Resumindo: uma raiz em + uma raiz em a função tem 2 raízes.
Passo 5
(b)
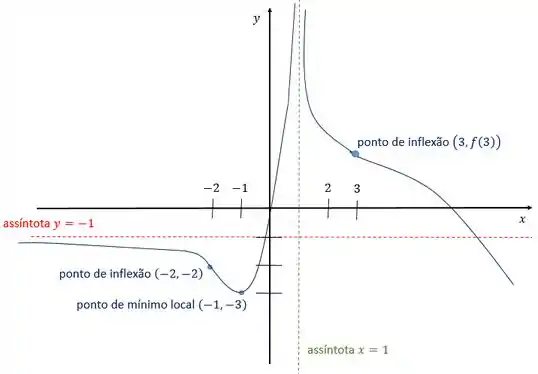
Repare que em , o sinal da derivada muda de pra , então o ponto é um ponto de mínimo local.
Além disso, em , o sinal da derivada segunda muda, também de pra , então o ponto é um ponto de inflexão. Ah, e também é ponto de inflexão, só não sabemos o valor de .
Outra coisa: como
Então é uma assíntota horizontal do gráfico.
Também temos uma assíntota vertical em , já que
Passo 6
Enfim, juntando todas as informações obtemos o esboço:
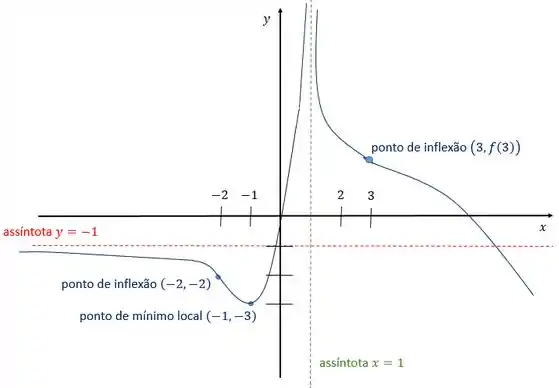
Resposta
(a)
tem 2 raízes.
(b)