Seja uma função contínua em . Suponha que o gráfico da derivada seja dado pela figura abaixo:
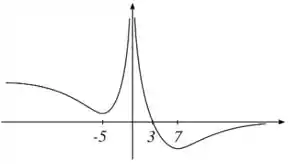
Considere as seguintes afirmações sobre o gráfico de :
é necessariamente um ponto de mínimo local.
é necessariamente um ponto de máximo local.
é necessariamente o valor máximo absoluto.
é necessariamente um ponto de inflexão.
Selecione a alternativa correta:
As afirmações e são verdadeiras e e são falsas
Todas as afirmações são falsas
As afirmações e são verdadeiras e e são falsas
Todas as afirmações são verdadeiras
As afirmações e são verdadeiras e e são falsas
Passo 1
Vamos juntos detonar essa questão!
Temos que avaliar o gráfico de e ver que informações podemos tirar sobre .
Quando o gráfico de passa pelo zero temos que vai ter um valor de mínimo ou máximo naquele ponto.
Quando temos valores máximos e mínimos no gráfico de temos geralmente pontos de inflexão em .
Sabendo disso vamos avaliar cada afirmação do enunciado.
Passo 2
Vamos começar com a .
Ela diz que é um ponto de mínimo local, mas se olharmos o gráfico de vemos que ela não passa por zero nesse ponto, então não tem como ter um ponto de mínimo em .
Essa afirmação é falsa.
Passo 3
Vamos analisar a .
Temos que ver se é um ponto de máximo local. Olhando o gráfico de vem que ela passa em zero nesse ponto, então já tem chances desse ponto ser um máximo, mas temos que garantir que ele é um máximo e não mínimo.
Para vermos isso vamos avaliar o valor de antes de e depois de , já que quando , temos uma crescente e quando temos temos uma decrescente.
Antes de a então está crescendo, depois de temos , então está decrescendo, então quer dizer que ela cresce até atingir um máximo em e depois decresce.
Então essa afirmação nos falou a verdade.
Passo 4
Agora vamos avaliar a .
Para que seja um máximo absoluto, então .
Mas olhando o gráfico de vemos que ela diverge pra , então quer dizer que também diverge nessa mesma situação, ainda mais que que não faz parte do domínio de .
Então não é sempre maior que um qualquer, logo a firmação é falsa.
Passo 5
Vamos para a última afirmação.
Temos que ver se é um ponto de inflexão, olhando gráfico de a gente ver que nesse ponto a função tem um mínimo, então ela tem um ponto de inflexão ali, então a afirmação é verdadeira.
Então temos que as afirmações e são verdadeiras e e são falsas, então nossa escolha da vez é a letra .
Resposta
As afirmações e são verdadeiras e e são falsas