Considere a função , definida para e
- Calcule
- Determine, se existirem:
- As assíntotas verticais e horizontais de ;
- Os intervalos onde é crescente e onde é decrescente;
- Os pontos de máximo e mínimo locais e/ou globais (abscissa e ordenada);
- Os intervalos onde tem concavidade para cima (convexa), concavidade para baixo (côncava) e os pontos de inflexão de ;
- Faça um esboço do gráfico de
Passo 1
a)
i)
Vamos começar calculando o limite pedido
Vamos olhar o limite de cada parcela da fração
Então
Passo 2
ii)
Vamos olhar o limite de cada parcela da fração
Então vamos ter uma indeterminação do tipo , vamos aplicar L’Hôspital
Passo 3
iii)
Não colocamos o sinal do infinito ainda, vamos discutir um pouco sobre isso.
Esse sinal depende apenas do limite do logaritmo, isso é porque ele vai para zero, que pode ser pelo lado direito ou esquerdo.
Como o valor de é menor que zero quando teremos
Então
Passo 4
iv)
Não colocamos o sinal do infinito ainda, vamos discutir um pouco sobre isso.
Esse sinal depende apenas do limite do logaritmo, isso é porque ele vai para zero, que pode ser pelo lado direito ou esquerdo.
Como o valor de é maior que zero quando teremos
Então
Passo 5
b)
i)
Como , para acharmos as assíntotas horizontais devemos fazer
Que já fizemos no item a
Então não temos assíntotas horizontais.
Passo 6
Para as assíntotas verticais devemos achar os limites nos pontos onde o denominador será zero, se esse limite der , ele será uma assíntota vertical.
No caso, é zero quando , já calculamos na letra a seu limite
Então é uma assíntota vertical.
Passo 7
ii)
Para olharmos se a função é crescente ou decrescente devemos calcular primeiro sua derivada
Aplicando a regra do quociente
Vamos agora analisar o sinal desta fração, fazendo o quadro de sinais. Antes devemos ver onde o numerador é zero e onde o denominador é zero.
No denominador, já vimos que
Enquanto isso, devemos resolver
Vamos ao quadro se sinais
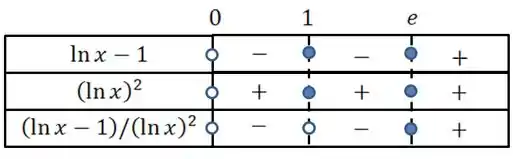
As “bolas” abertas significam q o ponto não está no gráfico.
Os intervalos onde a função é crescente são aqueles onde a derivada é positiva:
E decrescente onde ela é negativa:
Temos
Passo 8
iii)
Pelo quadro de sinais sabemos que quando a derivada muda de sinal temos um ponto de extremo local
Então
É um ponto de extremo local, como ele troca do negativo para o positivo ele é um mínimo local.
Passo 9
iv)
Para olharmos a concavidade devemos achar
Aplicando a regra do quociente
Passo 10
Vamos fazer o quadro de sinais.
Para isso devemos primeiro achar
Vamos ao quadro
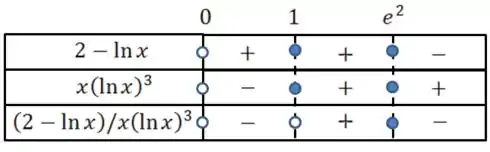
Temos
O ponto de inflexão acontece quando a concavidade muda, temos um pontos de inflexão
Passo 11
c)
O esboço do gráfico fica
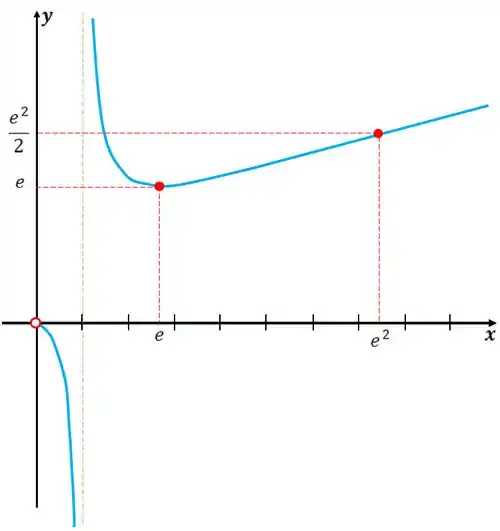
Resposta
Ei, a resposta está no passo a passo :)