Considere uma função tal que as suas três primeiras derivadas são contínuas e . Além disso, satisfaz as seguintes propriedades:
e não se anula fora de ;
.
O que se pode concluir a respeito da concavidade do gráfico de à direita e à esquerda de ? Faça um esboço de um gráfico compatível com essas informações. Justifique a sua resposta.
Passo 1
Opa! Vamos com calma nessa questão aqui, analisando cada um dos dados. A questão pediu o que podemos concluir a respeito da concavidade de na região de . Para tal, é interessante analisar a segunda derivada , mas também são úteis as demais derivadas.
Com isso, o problema nos deu . Isso nos leva a concluir que é raiz de e também é ponto crítico de .
Show, só que . Isso significa que também é um ponto de inflexão.
Além disso, não se anula fora de . Ou seja, para :
ou
Está bem, mas até aqui não pudemos concluir muita coisa.
Passo 2
O pulo do gato está justamente no fato de que . O que isso significa? Bem, se considerarmos outra função , então temos que:
Ou seja, é um ponto crítico de . Da mesma forma:
Ou seja, a segunda derivada de é positiva em . Se a segunda derivada é positiva e também é um ponto crítico, então, pelo teste da segunda derivada, é um ponto mínimo de .
Isso significa que à esquerda de e à direita de . Mas, ao mesmo tempo:
Logo, à esquerda de e à direita de . Ou seja, a função é côncava para baixo à esquerda de (carinha triste) e côncava para cima à direita de . (carinha feliz).
Passo 3
Já fizemos grande parte da questão, mas ainda precisamos dar um exemplo de função com essas propriedades.
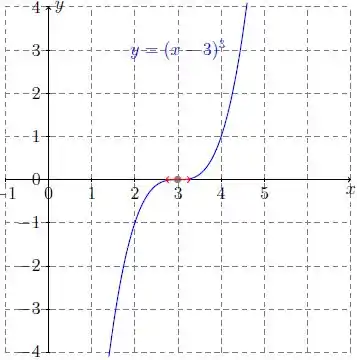
Repare que a função vai acumulando raiz, ponto crítico, ponto de inflexão etc. Um bom exemplo de função assim, é o . Por que? Porque:
No ponto :
Temos todas as propriedades dadas no problema, só que precisamos que isso seja verdade para . Para tal, vamos deslocar a função três unidades para direita:
Pronto! Chegamos na função que queríamos. Ela vai ter o mesmo gráfico de , só que deslocado três unidades para direita, como propomos na formação da função!
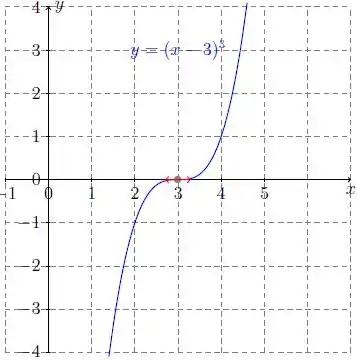
Resposta
A função é côncava para baixo à esquerda de (carinha triste) e côncava para cima à direita de .
É um bom exemplo para .