Considere a seguinte função
Encontre o domínio de , os pontos de interseção do gráfico de com os eixos e analise a simetria de .
Caso existam, determine as assíntotas horizontais e verticais de .
Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo e os seus valores.
Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de usando as informações obtidas nos itens anteriores.
Passo 1
Não existem restrições de domínio para essa função. Sendo assim,
Quanto às interseções, vamos fazer e ver que achamos e vice-versa:
A gente viu que intercepta o eixo e o eixo simultaneamente. Em outras palavras, intercepta os eixos na origem
Quanto à simetria da função, vemos que é um produto entre um função de simetria ímpar com uma sem nenhuma simetria , o que faz de uma função sem simetria.
Passo 2
As assíntotas verticais estão relacionadas com pontos de descontinuidades no domínio. Como vimos, o domínio é contínuo sempre, não havendo assíntotas verticais.
Para observar a existência das assíntotas horizontais vamos fazer os limites de para e :
Usaremos a Regra de L’Hospital nesse primeiro limite vezes para fugir da indeterminação
Achamos só uma assíntota horizontal, .
Passo 3
Para observar crescimento e decrescimento da função e seus mínimos e máximos devemos analisar o sinal da derivada primeira de . Vamos derivar a função que o enunciado deu então pela Regra do Produto:
Achamos, assim, a derivada de . Podemos ver que o termo será sempre positivo, já que é um produto de uma exponencial, que é sempre positiva, com um termo de expoente par. O sinal, portanto, só depende de , que será positivo para e negativo para . Assim, a função é crescente em e decrescente em , sendo um ponto crítico de máximo local, já que a derivada é positiva antes dele e negativa depois. Não há pontos de mínimo local.
Passo 4
Para observar a concavidade da função temos que olhar o sinal da derivada segunda. Vamos derivar pela Regra do Produto:
Vamos usar Bhaskara para descobrir as raízes de .
Podemos reescrever a derivada dessa maneira:
Fazemos um quadro dos sinais agora:
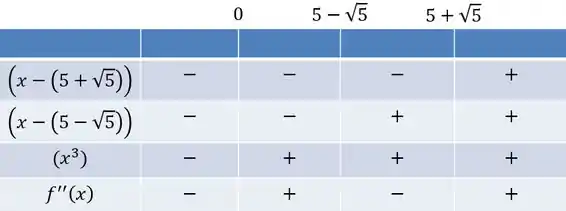
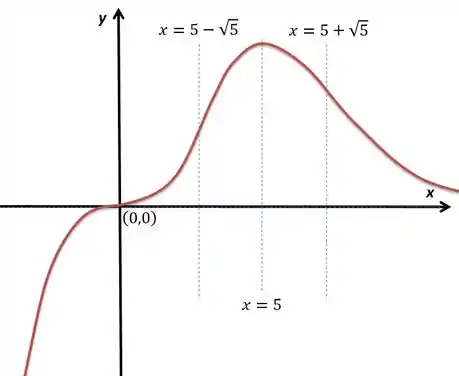
Vemos que tem concavidade para cima em e para baixo quando está em . Temos pontos de inflexão em e .
Passo 5
Vamos juntar todas as informações para esboçar o gráfico:
Vamos ao esboço: