Seja
Determine o domínio de
Determine os intervalos de crescimento e os intervalos de decrescimento de
Determine os pontos de máximo e de mínimo de
Determine todas as assíntotas da curva
Esboce o gráfico de contemplando tudo que foi calculado acima
Passo 1
No termo da função temos um limitante do domínio. Repare no seguinte, posso reescrever a função assim:
Por propriedade do logaritmo, coloco o expoente para fora:
Aqui é mais fácil de visualizar: o pede que seu argumento, , seja sempre maior que .
Com isso,
Passo 2
Vamos derivar pela Regra da Cadeia o termo que achamos no Passo :
Repare que é sempre positivo, pois é uma exponencial. Com isso, quem comanda o sinal da derivada e o crescimento da função é o . Não precisamos nem fazer o quadro de sinais desse termo, já que é um só:
Logo, a derivada é positiva para valores maiores que e negativa para valores menores que esse .
Dado isso, a função será crescente em e decrescente em , como indicado acima.
Passo 3
Para analisar os pontos de mínimo e máximo procuramos pontos de mudança do sinal da derivada. Quando vai de positiva para negativa, temos máximo. Quando negativa para positiva, temos mínimo.
Assim, é ponto de mínimo e não temos ponto de máximo.
Passo 4
Procuramos por assíntotas. Sabemos que as verticais estão relacionadas com descontinuidades no domínio. Sendo assim, vamos ver o limite lateral para na descontinuidade explode para :
Focando só no expoente:
Logo, não temos assíntotas verticais em e nem em nenhum outro ponto.
Passo 5
Vamos olhar agora por assíntotas horizontais. Como o domínio é , só fazemos para :
Não existem assíntotas horizontais, já que o limite explodiu para .
Passo 6
Agora partiríamos para o esboço. Antes vamos fazer a análise da derivada segunda, que nos dá informações sobre a concavidade do gráfico. Achamos a derivada segunda pelas Regras de derivação do Produto e do Quociente:
Repara, a função será sempre positiva no domíno , já que a exponencial e o termo ao quadrado são sempre positivos e terá sinal positivo quando .
Logo, concavidade sempre para cima
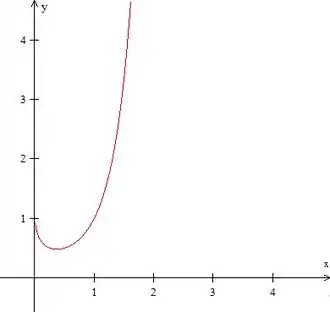
Agora, juntando tudo que vimos na questão, temos o seguinte:
Assim, o gráfico será: