Seja uma função derivável tal que:
- ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
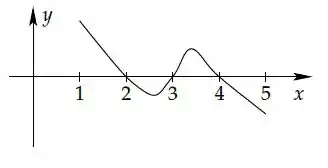
É correto dizer que o número de raízes de no intervalo é
Passo 1
Puts, um pouco enrolada essa questão. Muita coisa pra ver! Mas vamos com calma. Da esquerda pra direita, vamos analisar o que acontece, intervalo por intervalo:
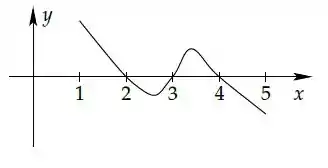
Começando por , nesse intervalo temos a assíntota vertical e vemos que a derivada, conforme o gráfico acima, é sempre positiva. Se a derivada é positiva em um intervalo, então a função é crescente, né não?
Pô, então a função tem assíntota em e não para de crescer até chegar em . O único jeito disso acontecer é se:
Uma coisa importante que a gente tem que pescar desse intervalo é que se a função vem lá do sempre crescendo, temos duas opções só possíveis:
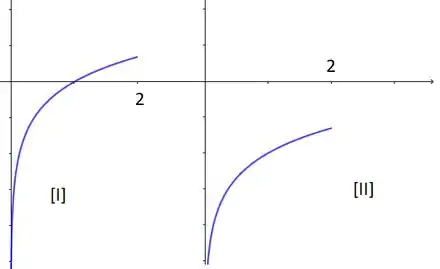
Ou seja, ou só temos uma única raiz, ou nenhuma. Só que se olharmos pro gráfico da derivada, vemos que em a função é estritamente decrescente (derivada negativa). Como , o único jeito de a função sair de descendo e alcançar é se . E se é esse o caso, fechamos o primeiro dos nossos intervalos, pois como:
Pelo TVI existe somente uma raiz no intervalo e o caso correto acima é o . Show de bola! Ainda de quebra provamos que no próximo intervalo não temos raízes. Afinal, se:
Não vai existir nenhum que faça
Passo 2
Belezinha, vamos pro próximo intervalo, o intervalo . Esse é até mais tranquilo, pois saímos de:
E seguimos crescendo e crescendo até chegar em . Isso porque em a função é estritamente crescente, evidenciado pelo fato que a primeira derivada é sempre positiva nesse intervalo. Sem raízes aqui também.
Agora vamos pro último intervalo e depois partir pro abraço! Ele vai ser . Nesse intervalo vemos que a função é estritamente decrescente, afinal, a primeira derivada é negativa nesse intervalo. Opa, já que ela é estritamente decrescente, e como sabemos que nesse intervalo ela sairá de cima do eixo , já que , temos três opções:
- A função sai lá do seu valor positivo e desce infinitamente, passando obrigatoriamente uma única vez só pelo eixo
- A função sai lá do seu valor positivo e desce até um certo ponto, chegando num limite finito e negativo, o que faz com que a função passe obrigatoriamente uma única vez só pelo eixo
- A função sai lá do seu valor positivo e desce até um certo ponto, chegando num limite finito e positivo, o que faz com que a função não toque nunca mais no eixo
Em matematiquês, isso é o mesmo que dizer que:
- A função possui assíntota pra
- A função possui assíntota horizontal negativa para
- A função possui assíntota horizontal positiva para
E olha só, como o enunciado diz que é uma assíntota, o primeiro caso é verdade! Graficamente é como se tivéssemos algo do tipo:
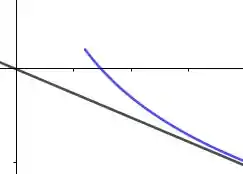
Então mais uma vez o gráfico de corta o eixo ! Como essa é nossa segunda raiz, fechamos a questão com chave de ouro se marcarmos a letra !