UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 10
Verifique que a trajetória , , é uma curva lisa cuja trajetória está contida na interseção do cilindro circular reto com a esfera . Esboce e e destaque a trajetória de .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma uma curva parametrizada que tá contida na interseção de um cilindro circular reto com uma esfera. Ele pediu pra gente verificar se essa curva (ou trajetória) é uma curva lisa, em seguida, plotar o cilindro, a esfera e a curva no gráfico.
Mas antes de mais nada, a gente precisa saber que uma curva dada por uma função vetorial em um intervalo é chamada de lisa se a derivada for contínua e se . Então, o que nós vamos fazer é calcular essa derivada e verificar as condições da curva. Em seguida, vamos esboçar o gráfico.
Vamos lá!
Passo 2
Vamos começar calculando a derivada da função vetorial , derivando cada componente de :
Nós sabemos que as funções seno e cosseno são contínuas, então a derivada da função também é contínua. Agora aplicando o parâmetro em , temos:
Então, temos , portanto, de acordo com a definição, a curva é lisa.
Passo 3
Agora, nós temos um cilindro circular reto de equação e uma esfera de raio , com equação . Com a ajuda de uma software nós plotamos essas superfícies:
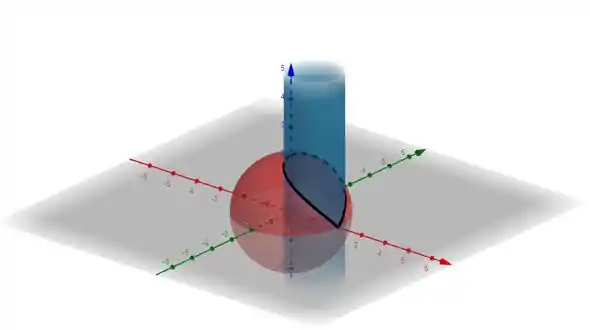
Repare que a curva em preto, na intereseção das superfícies, reprenta a curva paramétrica , como descrito pelo enunciado.
Valeu, galera! Até a próxima! 😉