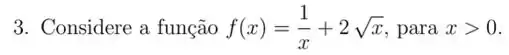
![]()
![]()
![]()
![]()
Passo 1
Primeiro, vamos olhar o domínio desse cara: a raiz quadrada a função não pode ter o . Além disso, o quociente do não pode ser nulo, então . Juntando tudo, temos que ter
Agora, para achar assíntotas horizontais, aplicamos o limite dessa para (não fazemos para , pois o domínio dessa função só comporta valores acima de ).
Sem assíntotas horizontais.
Para as assíntotas verticais, devemos aplicar o limite onde a função tem descontinuidades, ou seja, :
Temos assíntota vertical em .
Passo 2
Vamos analisar a derivada dessa função:
Assim, se como é sempre positivo, tudo agora depende de observar o . Esse termo zera para um valores de apenas:
Com isso, teremos apenas um ponto crítico. Como esse será negativo antes desse ponto e positivo depois, o ponto é de mínimo.
Enfim, a função vai ser crescente para , decrescente de até e tem um mínimo local em .
Passo 3
Vamos olhar a concavidade pela derivada segunda:
Repara que, no nosso domínio de , é sempre positivo. Logo, tudo depende de analisar o numerador dessa função: . Vamos ver onde ele zera:
Temos o como um termo que é negativo antes desse ponto de inflexão em e positivo depois que passamos dele.
Logo, tem um ponto de inflexão em , sendo côncava para cima de até e para baixo daí para frente.
Passo 4
Esboçando, nós teremos:
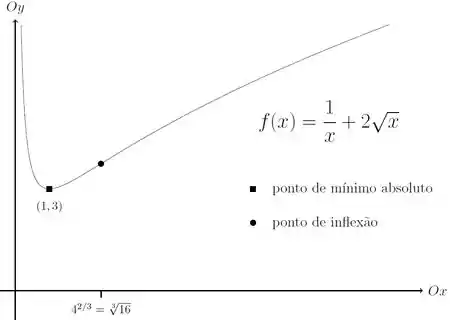
(esboço extraído do gabarito original)