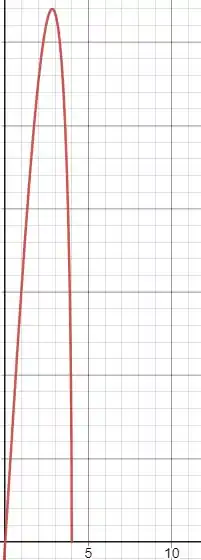
Conforme ilustra a figura abaixo, as áreas dos retângulos inscritos na circunferência podemos ser calculadas por meio da função , com
- Calcule os pontos críticos da função no intervalo
- Determine os intervalos de crescimento e os de decrescimento da função
- Determine os intervalos em que a concavidade do gráfico de é voltada para baixo e os intervalo em que a concavidade é voltada para cima
- Esboce o gráfico de
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Temos os retângulos inscritos na nossa circunferência, e queremos saber algumas coisas sobre ele, quando é nos dado a sua função da área. Veja como é:
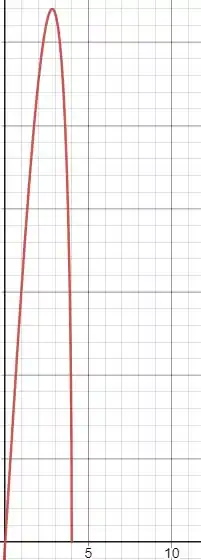
E se nos perguntarmos em que ponto de x a função é máxima. Ou a partir de que ponto ela cresce ou decresce? São essas duvidas que a questão nos pede para resolver.
Vamos lá?!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para a)
Para a)
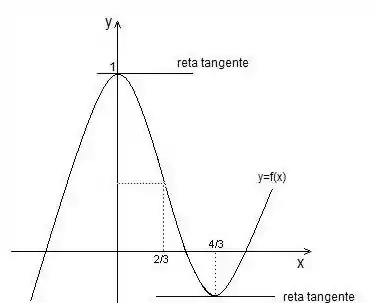
Um ponto critico é quando a derivada d função é nula. Por que nula? Porque é quando ela alcança o máximo ou o mínimo. Veja:
Assim, façamos a derivada:
Veja que aqui nós temos uma função composta, então assim temos que derivar pela regra da cadeia, ou seja ,assim:
Assim:
Podemos deixar tudo sobre :
Agora como dito, temos que igualando a 0:
Como então:
Passo 3
Para b)
Intervalos de decrescimento são intervalo onde a função cresce ou decresce, de forma que podemos saber a partir de qual ponto ela cresce ou decresce. Para isso, basta substituirmos o ponto que achamos quando igualamos a nossa derivada da função a 0 na própria derivada da função.
“Mas por que, Mogli?” pois se a derivada da função é 0 naquele ponto, em outras palavras ela é reta horizontal, significa dizer que antes dela e depois dela a função cresce e decresce, como na imagem anterior que demos:
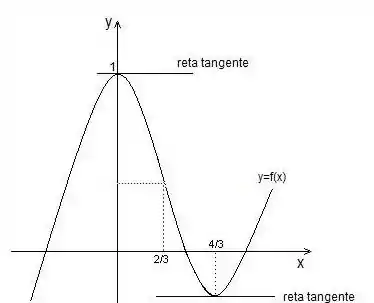
Repetindo a derivada:
E quando igualamos a 0, obtivemos: .Para sabermos de fato se a função cresce ou decresce naquele ponto, basta pegarmos quaisquer pontos nesse intervalo, se ela é maior que 0 significa que ela está crescendo, isso é chamado de varal de crescimento e decrescimento, e é dessa forma:
Escolhamos o ponto para o intervalo e o ponto para o intervalo . Ficando assim o varal:
Agora basta analisarmos o intervalo e verificar se é positivo ou negativo. Assim:
Mas veja que , de modo que:
Assim a função cresce no intervalo .
Para o outro intervalo:
Mas veja que , de modo que:
Assim a função decresce no intervalo .
Resumindo:
Passo 4
Para c)
Para a determinação do intervalo de concavidade de uma função devemos pegar a segunda derivada igualar a 0 e verificar se ela é positiva ou negativa. Para melhor visualização, veja essa imagem:
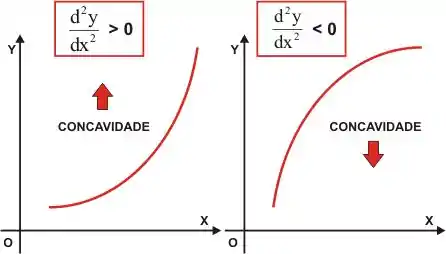
Ficou mais claro, né carinha?!
É parecido com o item anterior, não é?!
Sendo assim, derivemos a nossa função derivada de ou seja:
Como nós temos uma função de x em cima de uma outra função de x, devemos aplicar a regra do quociente, que é:
Chamemos então e
Assim:
Como temos uma função então assim temos que derivar pela regra da cadeia, ou seja ,assim:
Podemos deixar mais bonito, não?! Deixando tudo sobre , então:
Assim temos ao final:
Igualando a 0:
Considerando
Mas veja que e 4 é o limite que queremos, assim se a função é positiva ou negativa nesse ponto implica que a concavidade dela é inteiramente para cima ou para baixo, certo?!
Como não existe a função para , podemos pegar um ponto menor onde a função existe. Já que para qualquer ponto nela vai definir o seu todo. Seja
Assim:
Mas veja que assim a função é toda negativa no intervalo o que implica nesse caso que a concavidade é para baixo no intervalo
Resumindo:
Passo 5
Para d)
Kkkk sem queremos demos isso no passo 1 quando deduzimos o que que a questão pedia.
Mas fina que não demos hashushua
Sendo assim, considerando os itens acimas, com concavidade para baixo, ponto critico no ponto , obtemos um gráfico nessa pegada:
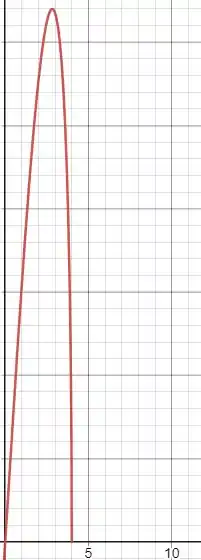
Obrigado por ter vindo até aqui, jovem mancebo. Até a próxima 😊
Resposta
Para a)
Para b)
Para c)
Para d)