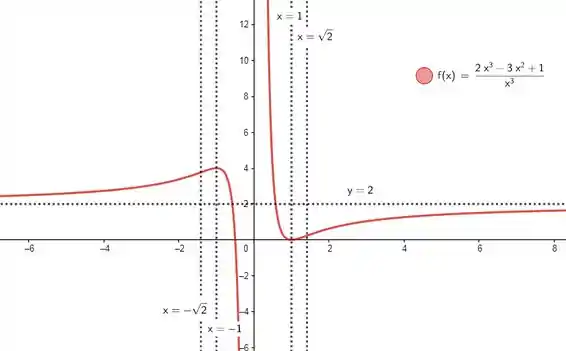
4) Considere a função , definida para
a) Determine as retas assíntotas verticais e horizontais (caso existam), calculando os limites necessários
b) Encontre os intervalos de crescimento e decrescimento, bem como os pontos críticos. Determine os pontos de máximo e mínimo locais, caso existam
c) Analise a concavidade e encontre os pontos de inflexão
d) Esboce o gráfico da função, destacando os pontos críticos e de inflexão, bem como as assíntotas
Passo 1
Vamo que vamo! Pra começar, vamos conversar sobre assíntotas. Começando pelas verticais, temos que ver o que acontece com os limites laterais pra valores de que “dão problema” na função. Como não da pra dividir nada por , é exatamente esse o valor que vamos usar! Mas antes, vamos dar uma arrumadinha na função:
Fazendo os limites laterais, temos:
Já que os dois limites explodiram, então tai! é uma assíntota vertical! Não temos outros candidatos, partimos então pra horizontal! Pra esses aí, a gente faz o limite pros infinitos e vê o que acontece. Saca só como fica:
Opa, se o limite pros dois infinitos deu um número, então nós temos duas assíntotas horizontais coincidentes. No caso, dá no mesmo dizer que a única assíntota que temos é
Concluímos:
Passo 2
Agora para falar de pontos de máximo e mínimo e intervalos de crescimento e decrescimento, não tem jeito! Precisamos da nossa querida amiga: a primeira derivada. Mudando um pouco a função pra facilitar, temos:
Derivando então:
Colocando tudo no mesmo denominador:
Como os pontos críticos são aqueles que zeram a primeira derivada ou fazem ela não existir, temos, além do , que não está definido, os pontos:
Vamos checar agora o sinal da primeira derivada em intervalos que envolvam os pontos críticos. Ou seja, vamos checar os intervalos:
Pro primeiro intervalo, vamos testar, por exemplo, :
Pro segundo intervalo, vamos testar, por exemplo, :
E opa! Se antes de a função era crescente (porque sua primeira derivada tinha sinal positivo) e depois se tornou decrescente (porque passou a ter primeira derivada com sinal negativo), é porque o ponto crítico é um ponto de máximo! Show, anotado!
Vamos partir agora pro teste do sinal no terceiro intervalo. Pra isso, vamos testar :
E pro último intervalo, vamos testar :
Aqui a gente já tem o inverso! Antes o sinal era negativo e depois passou a ser positivo! Então é um ponto de mínimo! Concluímos:
Passo 3
Pra gente fechar as análises e partir pro esboço, vamos agora falar de concavidade. Nossa amiga segunda derivada que será necessária agora. Calculando ela:
Colocando no mesmo denominador:
Pra gente analisar o sinal da segunda derivada, vamos ver em quais pontos ela zera e fazer intervalos envolvendo esses pontos e o ponto , uma vez que ele não está definido. Vamos ter:
Show de bola! Os intervalos que vamos checar serão:
Pro primeiro intervalo, vamos testar, por exemplo, :
Pro segundo intervalo, vamos testar, por exemplo, :
E opa! Se antes de a função tinha concavidade pra cima (porque sua segunda derivada tinha sinal positivo) e depois a concavidade ficou pra baixo (porque passou a ter segunda derivada com sinal negativo), é porque o ponto é um ponto de inflexão!
Vamos partir agora pro teste do sinal no terceiro intervalo. Pra isso, vamos testar :
E pro último intervalo, vamos testar :
De novo temos antes e depois com sinais diferentes! O que implica que também vai ser um ponto de inflexão!
Passo 4
Agora é só juntar tudo pra fazer o esboço:
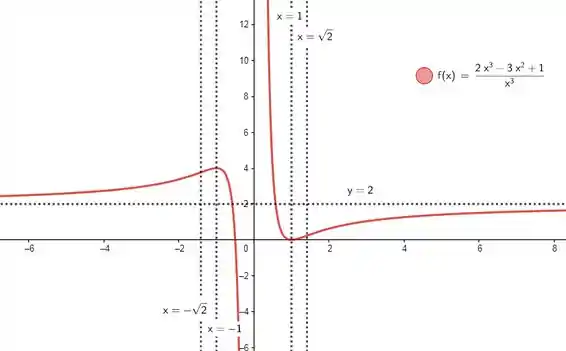
Resposta