4) Considere a função
- Calcule e
- Determine os intervalos de crescimento/decrescimento de , assim como os seus pontos (se existem) de máximo e mínimo absoluto/relativo.
- Determine os intervalos de concavidade para cima/baixo de g, assim como os seus pontos (se existem) de inflexão.
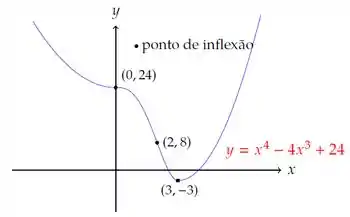
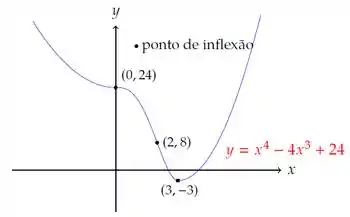
- Usando as informações dos itens anteriores, faça um esboço do gráfico de g, indicando os pontos notáveis obtidos. (Não tente determinar as raízes da função g.)
Passo 1
Bora lá, questão de esboço de gráfico. A letra está essencialmente pedindo pra gente ver se existem assíntotas horizontais. Mas veja bem:
Pô, é um polinômio! E polinômios não tem assíntotas horizontais! Em matematiquês, podemos provar isso fazendo:
O que dá:
Ou seja, os dois limites são iguais e não tem assíntotas horizontais!
Passo 2
Vamos então pra letra . Ela nos pede intervalos de crescimento e decrescimento. Quem dita isso é o sinal da primeira derivada. Então, derivando , temos:
Os pontos críticos vão ser aqueles que zeram a primeira derivada, logo:
E somente e fazem isso ser possível! Agora vamos analisar o sinal da primeira derivada em intervalos que envolvam esses pontos críticos, beleza? Os intervalos vão ser:
Pro primeiro intervalo, podemos testar . Vamos ter:
Pro segundo intervalo, podemos testar . Vamos ter:
Pro terceiro intervalo, podemos testar . Vamos ter:
Sendo assim, é decrescente nos dois primeiros intervalos (pois tem primeira derivada negativa) e crescente no último intervalo (pois tem primeira derivada positiva)
Agora vamos ver os pontos críticos. Pra , antes dele a função decrescia e depois a função continuava decrescente. Sendo assim, esse ponto não é nem de máximo nem de mínimo. Agora, pra , como antes dele a função decrescia e depois passou a crescer, vamos ter que:
Como os limites mostram que a função cresce indefinidamente pros dois lados, então:
Passo 3
Agora vamos bater um papo sobre concavidades. A analise é quase a mesma, mas agora com a segunda derivada. Logo, derivando uma vez a primeira derivada:
Temos:
E igualando a :
O que só é possível quando e . Agora vamos analisar o sinal da segunda derivada em intervalos que envolvam esses pontos, beleza? Os intervalos vão ser:
Pro primeiro intervalo, podemos testar . Vamos ter:
Pro segundo intervalo, podemos testar . Vamos ter:
Pro terceiro intervalo, podemos testar . Vamos ter:
Sendo assim, tem concavidade para cima no primeiros e último intervalo (pois tem segunda derivada positiva) e tem concavidade pra baixo no intervalo do meio (pois tem segunda derivada negativa)
Agora vamos ver os pontos que achamos. E veja só, tanto pra quanto pra a concavidade antes do ponto e depois do ponto são diferentes. Se são pontos de mudança de concavidade, são então pontos de inflexão!
Passo 4
Ta na hora de esboçar o gráfico. Já temos muita informação, saca só o resumo:
Caia bem saber as raízes, mas como essa questão não quer que a gente faça isso, vamos obedecer. Pra termos uma noção no entanto do que estamos fazendo, ao esboçar, vamos achar os pontos que envolvam os valores de notáveis que encontramos:
Opa, veja só! Se e , existe uma raiz entre e . Não importa onde é, mas no nosso esboço a curva tem que cruzar o eixo ! E ainda, como:
A partir do a curva vai cruzar outra vez o eixo ! Agora sim, mesmo sem saber as raízes, podemos esboçar direito. Vamos ter: