Considere a função dada por:
Determine caso exista(m):
(a.1) O(s) intervalo(s) de crescimento e decrescimento de
(a.2) O(s) valor(es) de para os quais a função possui máximo local e mínimo local.
(b.1) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
(b.2) O(s) ponto(s) de inflexão do gráfico de .
(c) Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão determinado(s) nos itens anteriores. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão
(d) A equação sempre possui solução? Justifique sua resposta.
Passo 1
O item tá pedindo o intervalo de crescimento e decrescimento e o , pontos de máximo e/ou mínimo. Quem vai ajudar a gente a responder os dois itens vai ser a inclinação da reta tangente, beleza? Como a inclinação é dada pela primeira derivada, partiu derivar!
E vamos lembrar do seguinte, se num intervalo qualquer, tivermos:
Opa, então pra gente saber em quais intervalos isso acontece, temos que igualar a primeira derivada à ! Vamos ter então:
Ou seja, vamos ter ou um ou o outro:
No último caso, dividindo os dois lados por , dá no mesmo. Ficamos com:
Como temos uma função de segundo grau, a gente pede ajuda pro famoso Bháskara! Afinal, se:
Podemos reescrever o polinômio como:
Onde são as raízes do polinômio, dadas por:
Vamos ter então:
Sendo assim
Beleza, achamos os pontos que zeram a primeira derivada! São eles:
E o que a gente faz com isso? Bem, a gente monta os seguintes intervalos envolvendo os valores encontrados:
E vê o que acontece com o sinal da primeira derivada nesses intervalos!
Passo 2
Vamos checar então o sinal da primeira derivada. No primeiro intervalo, , vamos escolher, por exemplo, . Vamos ter:
No segundo intervalo, , usando , por exemplo, vamos ter:
E pro terceiro intervalo, , usando , por exemplo, vamos ter:
Se no primeiro intervalo a primeira derivada é negativa, a função decresce. Se no segundo e no terceiro ela é positiva, então a função cresce. Show de bola, os intervalos vão ser:
Quanto a pontos de máximo e mínimo, seja:

Então olha só! Se e , o ponto se encaixa bem num ponto de mínimo: antes dele a função decrescia, depois, crescia!
O outro candidato seria , mas como antes e depois a função está crescento, não rola viu? Esse ponto não é de máximo e nem de mínimo, apesar de também ser um ponto crítico de .
Passo 3
Partiu então letra ! Bebe uma água e vem comigo que a gente tira a questão de letra! Como o item fala de concavidade e de ponto de inflexão, vamos usar agora a querida segunda derivada beleza? Olha só como ela vai ficar:
E vamos lembrar do seguinte, se num intervalo qualquer, tivermos:
Opa, então pra gente saber em quais intervalos isso acontece, temos que igualar a segunda derivada à ! Vamos ter então:
Dividindo de novo os dois lados por , temos:
Opa, outro polinômio de segundo grau! Partiu Bháskara de novo então! Vamos ter:
Então:
E reescrevemos o polinômio como:
Beleza, achamos os pontos que zeram a segunda derivada! São eles:
E o que a gente faz com isso? Bem, a gente monta os seguintes intervalos envolvendo os valores encontrados:
E vê o que acontece com o sinal da segunda derivada nesses intervalos!
Passo 4
Vamos checar então o sinal da segunda derivada. No primeiro intervalo, , vamos escolher, por exemplo, . Vamos ter:
No segundo intervalo, , usando , por exemplo, vamos ter:
E pro terceiro intervalo, , usando , por exemplo, vamos ter:
Maravilha, achamos os intervalos e os sinais! Como:

Vamos ter então:
E como o ponto de inflexão é exatamente o ponto em que a concavidade muda, vamos ter só dois pontos desse tipo, que vão ser:
Passo 5
Passo 5 é esboçar o gráfico e colocar, bem, tudo haha. Primeiro, vamos ver os pontos que devemos explicitar: os de máximo e mínimo e os de inflexão. Como
Vamos explicitar os pontos:
E explicitando também as retas tangentes a esses pontos, que tem a seguinte equação:
Onde é um ponto de tangência, vamos ter, para o ponto :
Para o ponto , temos:
E para o ponto , temos:
Pra fechar o esboço, dá uma olhada nisso:
Polinômios de grau par vão ter o mesmo limite, igual à , independente se ou se . Juntando isso com as informações que pegamos sobre intervalo de crescimento e decrescimento e concavidades, esboçamos:
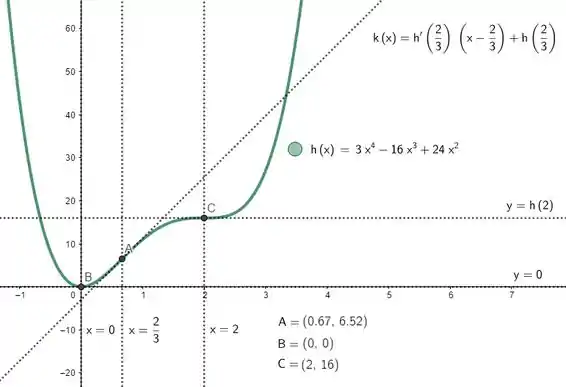
Passo 6
Pra fechar com chave de ouro, vamos resolver a letra . Quando pedimos pra checar se sempre tem solução, podemos reescrever a expressão para:
E checar a mesma coisa! Opa, então o que a questão quer saber é se, já que , a função tem como imagem todo o conjunto dos número reais. Mas veja bem: não assume valores negativos! Seja , por exemplo:
Se um exemplo desmente, então a equação da letra não tem solução sempre!
Resposta
(a.1)
(a.2)
(b.1)
(b.2)
(c) 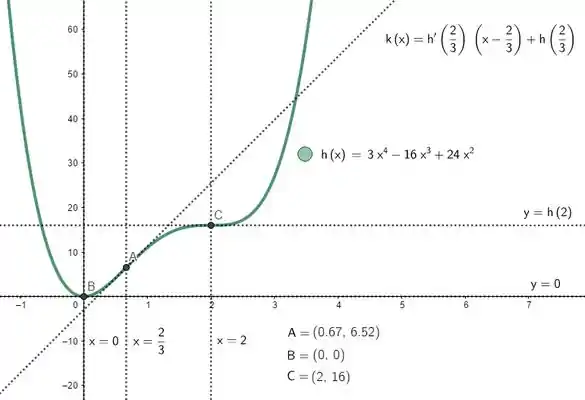
(d) Não, pois não assume valores negativos, por exemplo