Considere a função dada por:
(a) Determine caso exista(m):
(a.1) O(s) intervalo(s) de crescimento e decrescimento de
(a.2) O(s) valor(es) de para os quais a função possui máximo local e mínimo local. Atenção: só serão aceitas respostas com justificativas
(b) Determine caso exista(m):
(b.1) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo
(b.2) A(s) abscissa(s) do(s) ponto(s) de inflexão do gráfico de . Atenção: só serão aceitas respostas com justificativas
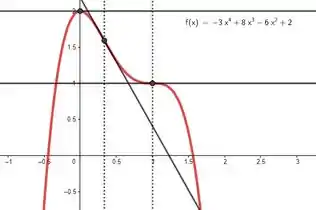
(c) Faça abaixo um esboço do gráfico de . Indique explicitamente em seu desenho as abscissas dos pontos de máximo, de mínimo e de inflexão determinados nos itens anteriores. Esboce também as retas tangentes ao gráfico de nos pontos em que a derivada é zero e nos pontos de inflexão.
Passo 1
Questão pacote completo em! Quer logo tudo sobre a função! Vamos pelo começo, vendo intervalos de crescimento e decrescimento. Pra isso galera, vamos precisar analisar o sinal da primeira derivada. Saca só:
Pra gente analisar o sinal, vamos primeiro ver em quais pontos ele muda igualando a primeira derivada a zero:
O que é o mesmo que:
Beleeeza, agora que achamos esses pontos, vamos analisar o sinal da derivada em intervalos que envolvam eles. Vamos ter:
Pro primeiro intervalo podemos testar, por exemplo, . Vamos ter:
Pro primeiro intervalo podemos testar, por exemplo, . Vamos ter:
Pro primeiro intervalo podemos testar, por exemplo, . Vamos ter:
Como a função é sempre decrescente quando a primeira derivada é negativa e crescente quando ela é positiva, os intervalos de crescimento e decrescimento são:
E bem, quando a função muda de crescente pra decrescente em um ponto, esse ponto é um de máximo. Oras! Temos isso em ! Veja no entanto que ponto de mínimo não teremos. Afinal, nenhum ponto faz a função sair de decrescente para crescente:
Passo 2
Bora agora ver então a análise de concavidade. Pra isso a idéia é quaaaase a mesma, ok? Diferença básica é que analisaremos o sinal da segunda derivada. Saca só:
Igualando a zero:
Opa, uma função de segundo grau que queremos achar as raízes? Tem cheiro de Bháskara em! Seja:
Vamos ter:
E finalmente:
Show, agora que achamos esses pontos, vamos analisar o sinal da derivada em intervalos que envolvam eles. Vamos ter:
Pro primeiro intervalo podemos testar, por exemplo, . Vamos ter:
Pro primeiro intervalo podemos testar, por exemplo, . Vamos ter:
Pro primeiro intervalo podemos testar, por exemplo, . Vamos ter:
E pronto! A função tem concavidade pra cima nos intervalos em que a segunda derivada é positiva e concavidade pra baixo nos intervalos em que ela é negativa, ok? Sendo assim, vamos ter:
E como os pontos de inflexão são exatamente aqueles pontos em que a função muda de concavidade, os dois pontos que achamos aqui são de inflexão!
Passo 3
E fechou pessoal, agora é só juntar tudo que achamos pra fazer um esboço maneiro da função. Lembre-se de desenhar as tangentes também!
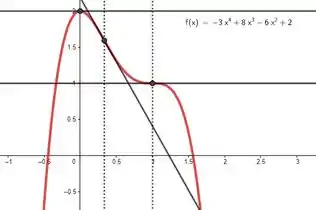
Resposta