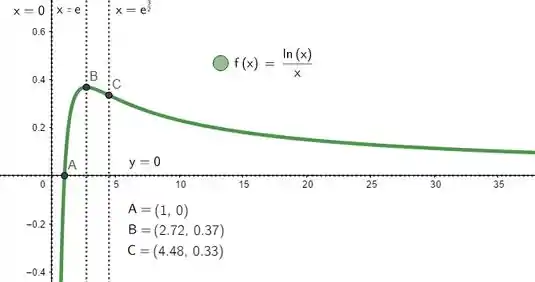
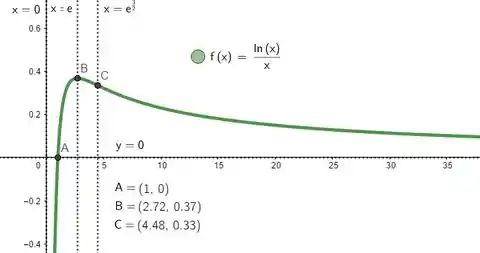
3) Considere a função
Determine, caso existam:
- O domínio da função
- As equações das assíntotas verticais do gráfico de
- As equações das assíntotas horizontais do gráfico de
- Os intervalos de crescimento e decrescimento de
- Os intervalos onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
- Utilizando as informações obtidas nos itens anteriores, esboce o gráfico da função . Marque em seu desenho as assíntotas verticais e horizontais e as abscissas dos pontos de máximo local, mínimo local e de inflexão do gráfico de , caso existam.
Passo 1
A questão quer da gente bastante coisa a respeito da nossa . Então vamos lá dar pra ela o que ela quer. Vamos começar com o domínio. Vendo bem a nossa função:
A gente vê que não rola! Veja bem, não podemos nem dividir nada por e também não tem como inserirmos valores menores ou iguais à dentro de . Sendo assim, o domínio de vai ser:
Beleza, primeira linha completa, vamos ver as próximas duas: as assíntotas! Começando pelas horizontais, pra gente ver se tem assíntotas, vamos ter que fazer o limite. Então partiu:
Perceba que não estamos nem ligando pra limite com porque o domínio não inclui valores negativos. Como o limite deu uma indeterminação do tipo , vai valer L’Hospital! Realizando LH então, ficamos com:
Opa, então temos sim uma assíntota horizontal! A reta:
Agora pra ver a vertical, como é uma fronteira aberta do domínio de , ele pode ser um bom candidato à assíntota vertical em! Calculando o limite então:
Opa, então temos mais uma assíntota, a reta:
Passo 2
Vamos ver agora tudo que envolva a primeira derivada de . Como essa derivada nos dá a inclinação da reta tangente ao gráfico, vai dar pra saber quando a função é decrescente ou crescente e em quais pontos ela troca entre eles. Derivando então:
Pela regra do quociente:
Beleza. Se a primeira derivada for positiva, a função é crescente. Se for negativa, decrescente. Então vamos igualar à e ver quando isso acontece:
Ok, uma raiz só na primeira derivada. Vamos checar o sinal dela então em intervalos que envolvam essa raiz e o domínio de . Os intervalos vão ser:
No primeiro, vamos testar por exemplo. Vamos ter:
E no segundo, vamos testar por exemplo. Vamos ter:
Opa, se antes de a função era crescente e depois se tornou decrescente, completamos então a tabela com as seguintes linhas:
Passo 3
Bora ver agora a concavidade. Pra isso, a gente vai precisar derivar de novo, beleza? A segunda derivada vai ser então:
Pela regra do quociente:
Igualando à , temos:
A ideia aqui é a mesma, beleza? Os intervalos que envolvem o valor encontrado e o domínio vão ser:
No primeiro intervalo, vamos testar por exemplo. Vamos ter:
E no segundo intervalo, vamos testar por exemplo. Vamos ter:
Como a concavidade é pra baixo no intervalo que a segunda derivada é negativa, vamos ter:
Já a concavidade pra cima ocorre quando a segunda derivada é positiva, logo:
E pra fechar com chave de ouro, como a concavidade só muda uma vez, o único ponto de inflexão vai ser exatamente
Passo 4
Terminamos a questão! Agora é só esboçar o gráfico. Enfim, ficamos com: