UFSCAR – Cálculo 1 – SUB – Questão 2
Considere a função
- Determine o domínio, a primeira derivada e estude o crescimento e decrescimento de
- Determine a derivada de segunda ordem, estude a concavidade de e determine os possíveis pontos de inflexão
- Determine, caso exista, os pontos críticos, de máximos locais, máximos globais, mínimos locais, mínimos globais de . Justifique o motivo de ser local ou global.
- Determine as assíntotas e faça o esboço na figura fornecida abaixo
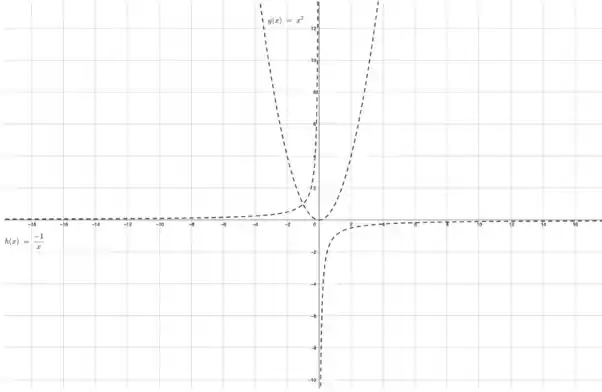
Passo 1
Oi, tudo bem? O problema nos deu essa função aqui
E perguntou uma série de itens: domínio, primeira derivada (crescimento/decrescimento, ponto de máximo/mínimo), segunda derivada (concavidade e pontos de inflexão), assíntotas e por fim o gráfico. Mas você lembra como encontrar todas essas coisas?
Vamos começar relembrando algumas coisas então:
- O domínio de uma função é o conjunto de entradas para os quais a função é real e definida. Então aqui é só investigar onde a função não existe e retirar dos reais!
- Em relação a primeira derivada temos: pontos críticos (onde a derivada primeira é zero), crescimento (), decrescimento (), pontos de máximo (sinal da derivada troca de ) e mínimo (troca de ). Então aqui a ideia é estudar o sinal da primeira derivada
- Em relação a segunda derivada temos: concavidades (positiva onde e negativa onde ) e pontos de inflexão: onde a curvatura troca de sinal!
- Verticais: analisamos o limite em torno da valores que explodem a função
- Horizontais: analisamos o limite da função indo para
Beleza?
Ainda temos as assíntotas,
E aí por fim juntamos todas essas informações e esboçamos um gráfico!
Mas relaxa, vou fazer com você!
Passo 2
Vamos começar com o domínio da função
Temos uma indeterminação quando , então nesse ponto a função não está definida!
Não temos mais outra (busque sempre por divisão por zero e raiz de índice par de número negativo, essas coisas não podem acontecer em funções reais!)
Logo nosso domínio são todos os elementos dos reais menos o zero
Beleza?
Passo 3
Agora vamos calcular a primeira derivada e os analisar o sinal de :
Derivando e igualando a zero:
Esse é nosso único ponto crítico! É onde a derivada é zero!
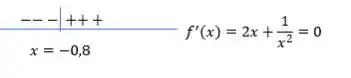Agora vamos analisar o sinal da função derivada em torno desse ponto:
Isso significa que em de , a função apresenta um ponto de mínimo local
Não sabemos se é (mínimo) global até fazer os limites no infinito.
Os intervalos de crescimento e decrescimento são:
Tudo bem até aqui? As análises envolvendo a primeira derivada acabaram, bora pra segunda?
Passo 4
Agora vamos analisar o sinal da função derivada segunda:
Derivando a igualando a zero temos:
Nosso candidato para ponto de inflexão é
Agora vamos analisar o sinal da função derivada segunda em torno desse ponto e em torno de , pois ali temos uma indeterminação
Vamos encontrar esse comportamento quando analisarmos o limite em torno de zero (assíntotas)
Vamos verificar a concavidade? Positiva (para cima) é onde a derivada segunda é positiva, e negativa (para baixo) onde ela é negativa
Passo 5
Nosso próximo passo é verificar as assíntotas!
- Começando pelas verticais: precisamos analisar o limite bilateral em torno da indeterminação da função:
- Assíntotas horizontais: investigar os limites em da função
Não temos assíntotas horizontais!
Passo 6
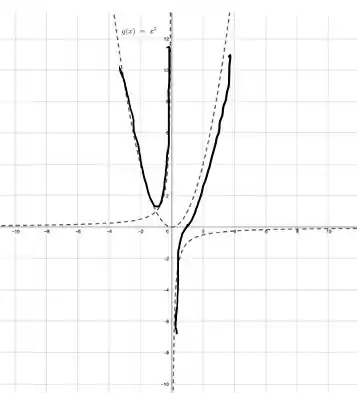Partiu juntar tudo isso e esboçar o gráfico? Juntando todas as informações e fazendo o esboço no gráfico que o problema deu temos o seguinte
Vemos que o comportamento é bem parecido com as tendências que ele alinhou! Ótimo! Agora vamos ver como ele fica em um software de gráfico mesmo (ninguém merece esse esboço feio feito à mão! haha)
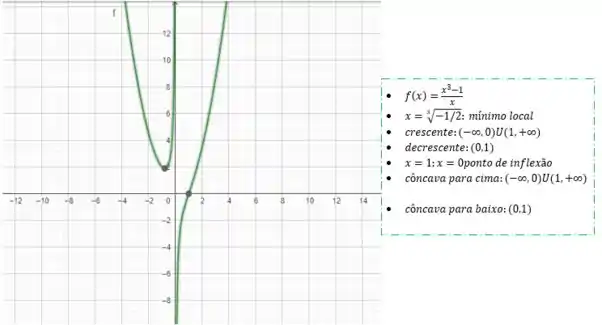
Então é isso pessoal! Terminamos!
Espero ter ajudado!
=D