Considere
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Passo 1
Vamos analisar a continuidade de em . Se for contínua analisaremos a continuidade de sua derivada no mesmo ponto para ver se é derivável. Façamos os limites laterais de acordo com a definição e vamos ver se bate a igualdade:
Ok, é contínua em .
Passo 2
Vamos ver se é derivável derivando suas duas leis de formação para cada intervalo do seu domínio:
Então também é derivável em !
Passo 3
Vamos calcular então e , de acordo com o domínio de cada intervalo da função :
Passo 4
Agora o outro limite:
Usamos L’Hospital para sair dessa indeterminação, botando a exponencial para ficar com uma indeterminação em forma de divisão:
Passo 5
Vamos determinar os pontos críticos de pela sua derivada que achamos na letra :
Vamos observar em cada intervalo pontos onde . Primeiro em :
Como temos que esse ponto é válido e é ponto de mínimo. Vamos olhar no outro intervalo, onde :
Nesse caso, vendo que o ponto é válido e é ponto crítico também.
Passo 6
Novamente, vamos dividir a análise aos dois intervalos e ver aonde cresce e onde decresce. Primeiro vamos observar o em . Olha, é sempre positivo, então o sinal só depende de , que é positivo quando e negativo antes.
A função é crescente em e crescente no intervalo .
No outro intervalo temos o domínio da derivada dado por . Esse termo é negativo quando e positivo quando .
Concluímos que é crescente em e decrescente em .
Juntando tudo notamos:
Passo 7
Vamos pegar os nossos dois pontos críticos e analisar a derivada antes e depois deles.
Em : temos que é decrescente antes e crescente depois: ponto de mínimo local.
Em : temos que é crescente antes e decrescente depois: ponto de máximo local.
Passo 8
A derivada segunda de pode ser obtida derivando cada domínio, o que ficaria assim:
Vemos que em a concavidade é sempre para baixo.
No outro intervalo o sinal só depende de , pois a exponencial é sempre positiva. Vemos que a é negativa antes de , positiva desse ponto e temos um ponto de inflexão em .
Resumindo:
Passo 9
Agora vamos desenhar de acordo com o que vimos aí a nossa :
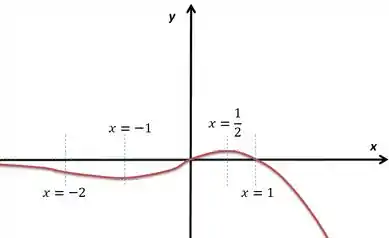
Cabô!