Q03) Considere a função
Determine caso existam:
- As equações das assíntotas verticais do gráfico de
- As equações das assíntotas horizontais do gráfico de
- As equações das assíntotas oblíquas do gráfico de
- Os intervalos de crescimento e decrescimento de
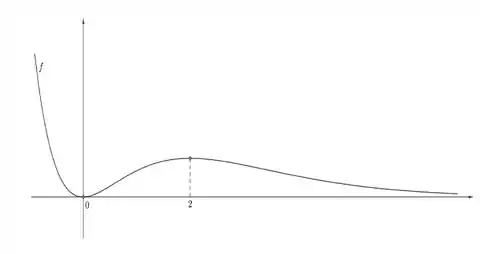
- Utilizando as informações obtidas nos itens anteriores, esboce o gráfico da função e suas retas assíntotas. Marque em seu desenho as abscissas dos pontos de máximo local e mínimo local do gráfico de , caso existam.
Passo 1
Bora começar. Na letra temos que descobrir eventuais assíntotas verticais do gráfico de . Pra entender, olha bem pra cara da função:
E olha só, ficou uma função dividida por outra nessa nova forma de escrever né? Então os pontos candidatos à assíntotas verticais são os que zeram o denominador, pois não estariam definidos. Mas err...
Não rola né, então se não tem como o denominador zerar pra qualquer que a gente escolha, a função está definida então em todo e não temos assíntotas verticais. Quanto as horizontais, temos que fazer:
Se esses limites derem números, ai sim teremos assíntotas hirozintais. Pro primeiro, saca só como fica:
Opa, indeterminação né? Mas como é do tipo , nada impede a gente de pedir ajuda pra L’Hospital, então realizando LH, temos:
Fazer L’Hospital uma vez não deu muito certo, mas pelo menos caímos no mesmo tipo de indeterminação, então bora de novo fazer LH:
Opa, achamos pelo menos uma assíntota horizontal. Agora pro outro limite, calculamos assim:
Como esse limite explodiu, a única assíntota horizontal mesmo é
Passo 2
Vamos checar agora as assíntotas oblíquas então. Pra isso vamos lembrar que, se ela existir, a equação será:
Tal que:
Perceba que não precisamos checar para já que já achamos uma assíntota pra esse lado, mas não pro outro. Achando então temos:
Esse limite tinha que dar um número! Se explodir pra então não temos assíntota oblíqua, ok? Até porque, não dá pra ter uma reta com coeficiente angular infinitamente grande e negativo, já pensou?
Passo 3
Bora pros intervalos de crescimento e decrescimento. E quem melhor pra nos ajudar nisso do que a primeira derivada? Afinal ela mostra a inclinação da reta tangete em determinado ponto. Então partiu derivar. Pela regra do produto:
Pra ver onde que a função cresce e decresce temos que trabalhar com o sinal da primeira derivada, porque a função cresce quando e decresce quando . Pra achar o ponto que isso muda, basta igualar à :
Bem, já que achamos dois pontos que zeram a primeira derivada, vamos testar o sinal dela em intervalos que envolvam esses pontos. Os intervalos vão ser:
Pro primeiro intervalo, vamos testar, por exemplo, . A primeira derivada fica:
Pro segundo intervalo, vamos testar, por exemplo, . A primeira derivada fica:
Pro terceiro intervalo, vamos testar, por exemplo, . A primeira derivada fica:
A conclusão que chegamos é:
Juntando essas informações com os limites hirozntais, temos o suficiente pra esboçar o gráfico. Então partiu!