3) repita o que foi feita no feito no exercício acima para as funções seguintes;
d)
Passo 1
Fala aí, galerinha!! Nesse exercício ele pede para a gente obter uma série de coisas:
- Pontos críticos,
- Máximos e mínimos locais,
- Intervalos de crescimento e decrescimento,
- Pontos de inflexão,
- Intervalos onde é côncava para cima e para baixo
- Determinar as (possíveis) assíntotas
- Fazer um esboço do gráfico.
NOSSA! Um monte de coisa... mas relaxa que a gente fazendo cada um dos passos aqui isso vai sair bem de boa. Todos esses itens estão relacionados com as derivadas da função. Então a gente começa calculando essas derivadas! No geral a primeira derivada dá conta da maioria dos itens, mas não vamos esquecer que a segunda derivada também ajuda bastante então é legal começarmos calculando as duas!
Passo 2
Vamos começar calculando as derivadas de
Nós temos uma função composta então a gente usa a regra da cadeia:
Passo 3
Também é bem útil começar obtendo a derivada de segunda ordem. Fazemos isso derivando a função:
Agora temos um produto de funções. A gente resolve essa derivada usando a regra do produto:
Então temos
Arrumando um pouco temos:
Showw, agora a gente usa essas derivadas nos testes para obter cada um dos itens que nos pediram!
Passo 4
Vamos começar com os pontos críticos. Esses pontos são aqueles em que a primeira derivada é zero:
Aqui temos duas possibilidades: ou e isso já nos dá o primeiro ponto crítico:
A outra possibilidade é
Só que a função exponencial nunca zera. Então não temos nenhum nesse caso!
Passo 5
Uma vez que a gente possui as derivadas e o nosso ponto crítico vamos classificar esse ponto em um máximo ou mínimo local ou em um ponto de inflexão. Para ver se é um máximo ou mínimo local, vamos ver o sinal da segunda derivada nesse ponto:
Como a segunda derivada no ponto crítico é negativa, é um máximo local de !
Como essa função não possui outros pontos críticos, não temos um mínimo local e nem um ponto de inflexão!
Passo 6
Para ver sobre o intervalo de crescimento ou decrescimento olhamos os sinais de . Quando esse cara é positivo, a função é crescente e quando é negativo a função é decrescente.
Vamos olhar a cara de
Como a exponencial sempre resulta em um número positivo, quem manda no sinal da função é aquele termo , então temos
- quando e a função é crescente nesse intervalo;
- quando e a função é decrescente nesse intervalo.
Passo 7
Agora, para olhar sobre a concavidade, olhamos o sinal da segunda derivada
Aonde temos a regra:
Como a exponencial sempre resulta em um número positivo, quem manda no sinal da função é aquele termo , então a função vai ser concava para cima se
E vai ser concava para baixo quando
Como a função muda a concavidade em e , esses são os pontos de inflexão da função!
Passo 8
Para olhar as assíntotas a gente deve olhar dois casos:
Assíntotas verticais: Quando temos um onde
Pela cara da nossa função, vemos que ela nunca diverge (geralmente isso acontece quando temos uma fração com um polinômio no denominador). Essa nossa função não tem assíntota vertiacal então.
Assíntotas horizontais: A gente calcula os limites:
Então uma assíntota horizontal em . Shoow
Passo 9
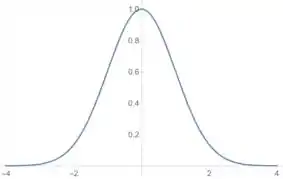
Para esboçar essa função a gente junta todas essas informações que a gente obteve, marca as assíntotas horizontais no plano cartesiano, marca o máximo que a gente encontrou e usa os intervalos de concavidade para fazer o esboço. Fica mais ou menos assim:
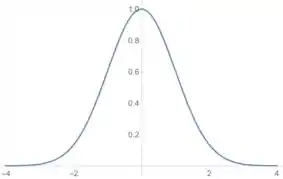
Resposta