1) Seja dada por
Esboce o gráfico de localizando intervalos de crescimento e decrescimento, concavidades, limites convenientes e assíntotas (quando existirem). Use que:
Passo 1
Felizmente pra essa questão vamos ter um trabalho a menos: não vamos precisar derivar. Então pra esboçar, vamos começar a catar informaçõessobre a função. A começar pelas interseções com os eixos. Se , vamos ter:
Se , vamos ter:
São pontos então da curva:
Passo 2
Agora vamos falar de assíntotas. Pra isso, temos que calcular limites. A começar com assíntotas horizontais, vamos ter:
Calculando o primeiro limite, temos:
Aplicando L’Hospital, vamos ter:
Para o segundo limite, vamos ter:
Por fim, chegamos à:
Agora vamos olhar pro outro lado e fazer o limite , beleza? Ficamos com:
Resumindo a ópera, vamos ter somente uma assíntota horizontal, e vai ser a reta:
Passo 3
Agora pras assíntotas verticais, vamos ver em quais pontos a função “dá problema”. Como temos duas razões de polinômios: uma multiplicando a exponencial:
E outra dentro da exponencial:
O único ponto que dá problema é aquele que zera o denominador. Nos dois casos vão ser:
Então bora fazer o limite para essa valor. Primeiro tendendo pela esquerda, vamos ter:
Pro primeiro limite, ficamos com:
E no segundo limite:
Juntando tudo, achamos o limite:
Só que não acabou ainda viu? Temos que ver o limite com tendendo pela direita. Nesse caso, calculamos:
Veja bem, apesar de os limites calculador pela esquerda e pela direita não terem dado a mesma coisa, pelo menos um deles deu . Sendo assim, podemos confirmar sim:
Como única assíntota vertical
Passo 4
Bora falar de intervalos de crescimento e decrescimento agora. Uma função cresce quando sua primeira derivada é positiva e decresce quando negativa, pois o sinal dela dá a inclinação da reta tangente. Como:
Vamos achar os valores de que fazem ser pra depois estudar os sinais, ok? Bora lá:
Beleza, agora que achamos o valor de que zera, vamos testar o sinal em intervalos que envolvam esse ponto e a assíntota vertical. Os intervalos vão ser:
Pro primeiro intervalo, escolhendo, por exemplo, , temos:
Pro segundo intervalo, escolhendo, por exemplo, , temos:
Pro terceiro intervalo, escolhendo, por exemplo, , temos:
Fechamos então os intervalos:
E veja bem. Como a função é crescente em e depois em decresce, vamos ter então que o ponto crítico é um ponto de máximo.
Passo 5
Chegamos na hora da concavidade! A ideia é a mesma do passo 4, só que vamos usar a segunda derivada:
Pra ela ser zerada, temos que:
Pela fórmula de Bháskara, seja:
Onde:
Vamos ter:
Reescrevemos o polinômio para:
E os valores que zeram vão ser exatamente:
Beleza, achamos os pontos que zeram. Incluindo agora o valor da assíntota vertical , basta a gente montar os intervalos pra checar. Eles vão ser:
Pro primeiro intervalo, escolhendo, por exemplo, , temos:
Pro segundo intervalo, escolhendo, por exemplo, , temos:
Pro terceiro intervalo, escolhendo, por exemplo, , temos:
Pro quarto intervalo, escolhendo, por exemplo, , temos:
Quando um intervalo tiver sinal negativo, é porque a concavidade está pra baixo. Quando tiver positivo, concavidade pra cima. Ficamos então com:
E como os pontos de inflexão são exatamente os pontos que fazem a concavidade mudar, vamos ter como pontos de inflexão:
Passo 6
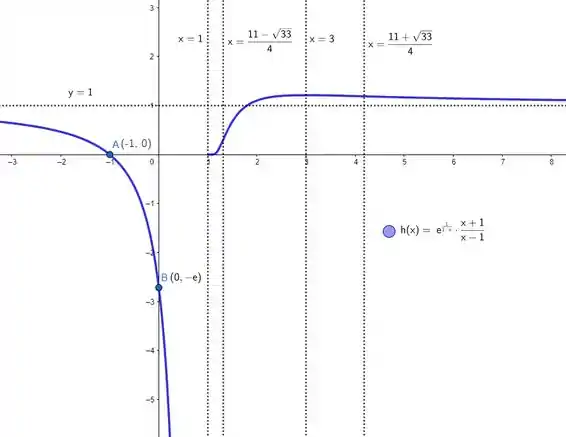
Ufa, calculamos tudo. Agora vamos juntar todas as infos pra poder esboçar o gráfico. Temos:
Misturando essas coisas todas aí, esboçamos:
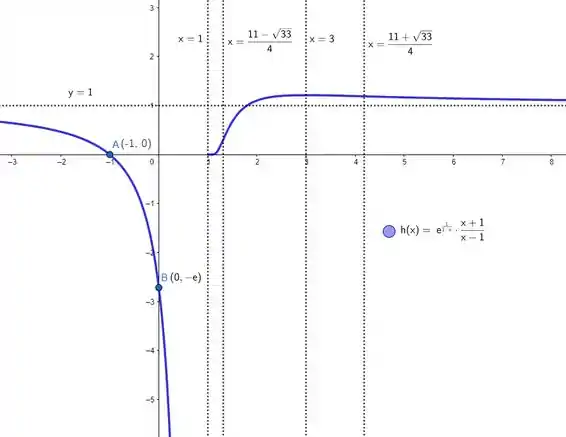
Resposta