Seja :

Mostre que e que .

Encontre o domínio de .

Encontre os interceptos de com os eixos coordenados.

Analise a simetria de .

Caso existam, encontre as assíntotas horizontais e verticais de .

Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo/mínimo.

Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.

Esboce o gráfico de usando as informações obtidas nos itens anteriores.

Como os termos e não tem descontinuidades, o domínio é .

Para achar os interceptos temos que fazer e :

Só encontramos um ponto, ou seja, ele corta a origem que é o encontro dos eixos.

Como é um produto entre uma função par e uma sem simetria nenhuma concluímos que não terá simetria par ou ímpar.

Como não temos descontinuidade no domínio, concluímos que não existem assíntotas verticais. Quanto às assíntotas horizontais, vamos usar o limite quando :

Concluímos, pelos limites, que existe uma assíntota horizontal em quando .

Para analisar o crescimento da função temos que observar quando a função é positiva ou negativa. A função derivada é , onde é sempre positivo. Assim, o sinal só depende da parábola:

Como vemos, é uma parábola com concavidade para cima e raízes em e . Notamos, com isso, que só será negativo entre e , sendo positiva no resto do domínio.

é um ponto crítico de máximo, já que a derivada é positiva antes dele e negativa depois.

é um ponto crítico de mínimo, já que a derivada é positiva antes dele e negativa depois.

A função é crescente para todo fora do intervalo , onde é decrescente.

A derivada segunda de é

Sendo que é sempre positivo. Assim, o sinal só depende de , uma parábola com a concavidade para cima e raízes, por Bhaskara, em:

Assim, vemos que a será negativa e a concavidade será para baixo quando estiver entre e . No resto do domínio, a concavidade é para cima.

e são pontos de inflexão.

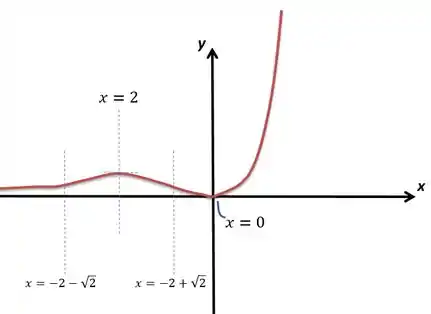
Juntando as informações:

Esboçando, fica assim: