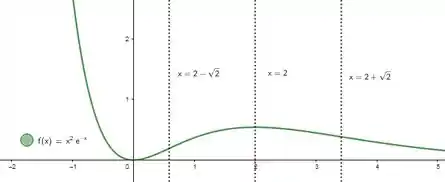
Seja a função definida por .
(a) Encontre as assíntotas verticais e horizontais caso existam;
(b) Encontre os intervalos onde a função é crescente e onde é decrescente;
(c) Encontre os valores de máximo e mínimo locais;
(d) Encontre os intervalos de concavidade e os pontos de inflexão
(e) Use as informações acima para fazer um esboço do gráfico de
Passo 1
Essa é daquelas questões boazinhas que já nos dão o passo a passo. Então vamos começar com as assíntotas dessa função. Pras horizontais, temos que fazer:
Então partiu. Para
Eita! Indeterminação! E agora? Caalma gafanhoto, essa daí é do tipo que da pra resolver por L’Hospital. Então se derivarmos em cima e em baixo, vamos ter:
Outra indeterminação! Bom, já que ela caiu numa do mesmo tipo da anterior, por que não realizar L’Hospital novamente? Fazendo LH então:
Show! Achamos uma assíntota horizontal: a reta . Pra vermos se tem outra basta fazer agora:
Dessa vez não rolou! O limite não deu um número então só vamos ter uma assíntota horizontal mesmo. Agora, pras verticais, dá uma boa olhada na função:
Po, se não tem nenhum valor de que eu escolha que eu não consiga arranjar um de volta pra mim, então não temos candidatos a pontos que “dão problema” na função. Isso, na prática, é sinal de que não existem assíntotas verticais!
Passo 2
Pros intervalos de crescimento e decrescimento agora o bicho pega, porque precisamos derivar! Como nossa função pode ser entendida como um produto de duas funções, usando a regra do produto:
Pra gente ver intervalos de crescimento e decrescimento temos que analisar o sinal da primeira derivada. Se positiva, a função cresce, se negativa, decresce, tranquilo? E pra isso, vamos ver em que pontos que ela muda de sinal:
Então podemos testar o sinal da primeira derivada em intervalos que envolvam esses pontos. Eles vão ser:
Pro primeiro intervalo, podemos testar, por exemplo, . Vamos ter:
Pro segundo intervalo, podemos testar, por exemplo, . Vamos ter:
Pro terceiro intervalo, podemos testar, por exemplo, . Vamos ter:
Analisando esses resultados, concluímos que:
Como do primeiro pro segundo intervalo a função passa de decrescente pra crescente, então na fronteira desses intervalos, em , temos um ponto de mínimo e como do segundo pro terceiro intervalo a função passa de crescente pra decrescente, então na fronteira desses intervalos, em , temos um ponto de máximo. Bora pro próximo item agora!
Passo 3
Agora a gente vai partir pra análise da concavidade. A ideia é a mesma do passo anterior, só que agora com a segunda derivada da função. Então partiu derivar a primeira derivada! Vamos ter:
E derivando cada um dos termos:
Pra gente ver os intervalos que a segunda derivada mudam de sinal a gente vê a fronteira desses intervalos primeiro. Pra isso, igualando a zero e fazendo Bháskara:
Onde:
Os intervalos que vamos testar vão ser então:
Pro primeiro intervalo, podemos testar, por exemplo, . Vamos ter:
Pro segundo intervalo, podemos testar, por exemplo, . Vamos ter:
Pro terceiro intervalo, podemos testar, por exemplo, . Vamos ter:
Analisando esses resultados, como o sinal positivo indica concavidade pra cima e o negativo, concavidade pra baixo, concluímos que:
E os pontos de inflexão vão ser exatamente aqueles valores de em que a concavidade muda, belezinha? Eles serão então:
Passo 4
E agora a gente fecha com chave de ouro esboçando tudo. Nossos resultados, resumindo, foram:
Esboçamos então:
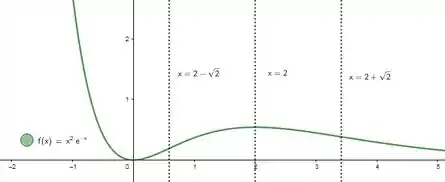
Resposta