Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Passo 1
O primeiro passo é definir o domínio de , isto é, o conjunto dos valores de para os quais está definida. Temos neste caso que o denominador não é definido se for igual a zero, então podemos escrever que:
Assim, temos que:
Passo 2
Agora devemos definir as intersecções com os eixos. Para o eixo a interseção é dada por e para o eixo fazemos e isolamos o .
Assim, temos que:
Logo a função passa pela origem.
Passo 3
Devemos verificar se a função possui simetria. Temos três casos:
- Se para todo em , é uma função par e a curva é simétrica em relação ao eixo . Caso isso ocorra basta refletir a curva em torno do eixo para obter a curva completa.
- Se para todo em , é uma função ímpar e é simétrica em relação à origem. Caso isso ocorra basta girar a curva em em torno da origem para obter a curva completa.
- Se para todo em , onde é uma constante positiva, é uma função periódica e o menor desses números é chamado de período. Caso isso ocorra pode-se usar a translação de um período para esboçar o gráfico inteiro.
Tomando temos:
- Não possui período.
Logo a função não possui simetria.
Passo 4
Devemos verificar agora se a função possui assíntotas:
- Assíntota horizontal:
- Assíntota vertical: a reta é uma assíntota vertical se pelo menos uma das seguintes afirmativas for verdadeira:
Se então a reta é uma assíntota horizontal da curva .
Se resultar que , então não temos uma assíntota à direita.
Temos:
Assim, não há assíntota horizontal .
Tomando , temos:
Logo, temos uma assíntota vertical em .
Passo 5
O próximo passo é definir os intervalos de crescimento ou decrescimento da função. Calculamos e encontramos os intervalos nos quais é positiva ( é crescente) e os intervalos nos quais é negativa ( é decrescente) .
Derivando temos:
Então, , assim é decrescente em e e crescente em .
Passo 6
Calcularemos agora os pontos críticos, números em que ou . Aplicando o Teste da Derivada, se muda de positiva para negativa em um número crítico , então é um máximo local. Se muda de negativa para postiva em , então é um mínimo local.
Temos que:
Observamos que a equação é satisfeita para e esse ponto não está definido na função, logo não possui é um ponto crítico; e para , o qual pode ser. Vamos então analisar um ponto antes e depois dele:
Logo a função descresce antes de e cresce depois dele, sendo então um ponto de mínimo.
Passo 7
Calcularemos agora a concavidade da função utilizando . Se a função é côncava para cima e se a função é côncava para baixo.
Assim temos que:
Então é côncava para baixo com no intervalo de e côncava para cima com nos intervalos e .
Passo 8
Passo 9
Passo 10
Passo 11
Passo 12
Passo 13
Por fim, esboçando a curva obtemos:
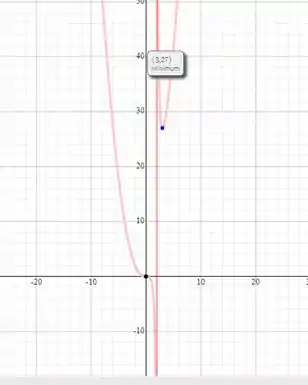
Resposta
Ei, a resposta está no passo a passo :)