Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes por Integrais Duplas

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990

Enunciado

  1. Calcule o Volume do sólido contido no primeiro octante, limitado pelo cone   z = r , pelo cilindro r = 3 sin ⁡ θ e pelo plano z = 0 .

Passo 1

Cara, eu sei que o exercício está meio louco, mas pensa comigo: ele te deu superfícies em termos de r e θ o que isso pode significar? Sim! As coordenadas polares!

x = r cos ⁡ θ

y = r sin ⁡ θ

Não se esqueça da equação da circunferência...

x 2 + y 2 = r 2

e nem do Jacobiano quando estivermos na integral:

J = r

Passo 2

Pow! Precisamos colocar aquelas superfícies do enunciado em termos das coordenas retangulares (em termos de x e y ). Para isso, vamos apenas substituir, veja:

C o n e           ⇒ T e m   e q u a ç ã o …             z = r

logo...

z 2 = r 2

substituindo então obtemos

z 2 = x 2 + y 2

Que de fato é um cone comum representado dessa forma:

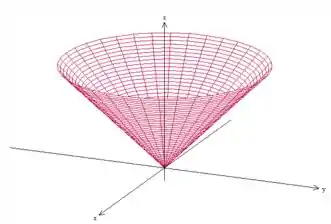
Outra superfície que podemos fazer o mesmo é com o cilindro r = 3 sin ⁡ θ :

r = 3 sin ⁡ θ               ⇒ M u l t i p l i c a n d o   p o r     r e m   a m b o s   o s   l a d o s …                       r 2 = 3   r sin ⁡ θ

Substituindo então...

x 2 + y 2 = 3 y

Pow! Essa é a equação do cilindro, mas está difícil de enxergar, neh? Por isso, vamos completar quadrado com ele aqui...

x 2 + y 2 - 3 y = 0

Como y - 3 2 2 = y 2 - 3 y + 9 4 ...

x 2 + y 2 - 3 y + 9 4 - 9 4 = 0       →           x 2 + y - 3 2 2 = 9 4

De fato é um cilindro de raio 3 2 deslocado um pouco em y .

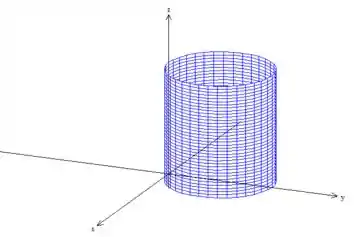
Como estamos trabalhando no primeiro quadrante, então o sólido é esse aqui:

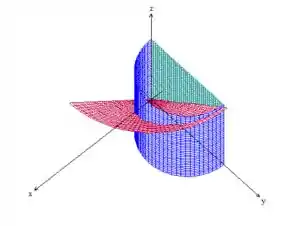
Passo 3

Pow! O problema nos pediu um volume de sólido, e a essa altura, podemos calcular um volume utilizando uma... I n t e g r a l   D u p l a   : )

V o l u m e = ∬ D   f x ,   y d A

Porém, como estamos trabalhando dentro de um cilindro e os dados já foram dados em coordenadas polares, é muito válido a gente transformar para a integral nessas coordenadas:

Não se esqueça de multiplicar pelo Jacobiano, heim!

V o l u m e = ∬ D   f x ,   y d A = ∬ D r θ   f ( r , θ ) ∙ J d r d θ

Mas veja que para resolver essa integral aí necessitamos de algumas informações:

  • Quem é o f ( r ,   θ ) ?
  • Quem é a região de integração em termos de r e θ D r θ ?

Para ambas as perguntas, vamos encontrar as respostas no esboço do sólido no espaço novamente:

Epa! A função f que vamos integrar é o próprio cone com e q u a ç ã o :

f r ,   θ = z = r

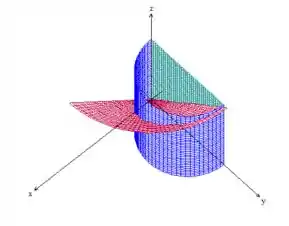
Quanto à outra pergunta... me siga!

Passo 4

Bem, a região em que estamos integrando está na sombra desse sólido:

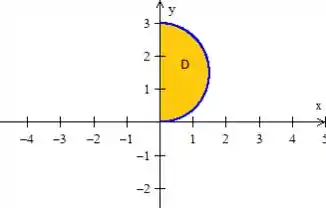
Logo, em coordenas polares, notamos que

0 ≤ r ≤ E q u a ç ã o   d o   c i l i n d r o

0 ≤ r ≤ 3 sin ⁡ θ

enquanto isso, o ângulo θ ... esse cara aqui, oh:

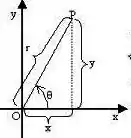
ele só pode estar indo do 0 até 90   ° afinal de contas estamos apenas trabalhando apenas no primeiro quadrante

0 ≤ θ ≤ π 2

Passo 5

Montando a integral então...

∫ 0 π 2 ∫ 0 3 sin ⁡ θ r ∙ J d r d θ =

∫ 0 π 2 ∫ 0 3 sin ⁡ θ r 2 d r d θ

Agora é só calcular essa integral aí normalmente...

∫ 0 π 2 ∫ 0 3 sin ⁡ θ r 2 d r d θ = ∫ 0 π 2 ∫ 0 3 sin ⁡ θ r 2 d r d θ

Calculando a integral de dentro...

∫ 0 π 2 r 3 3 0 3 sin ⁡ θ d θ =

∫ 0 π 2 3 sin ⁡ θ 3 3 d θ = 9 ∫ 0 π 2 sin 3 ⁡ θ d θ

Bora calcular essa integral? (vamos trabalhar com ela indefinida aqui apenas para não atrapalhar o raciocínio):

∫ sin 3 ⁡ θ d θ =

Como o coeficiente do seno é impar, podemos separar dessa forma

∫ sin 2 ⁡ θ sin ⁡ θ d θ →

onde lembrando que sin 2 ⁡ θ = 1 - cos 2 ⁡ θ ...

∫ 1 - cos 2 ⁡ θ sin ⁡ θ d θ =

∫ sin ⁡ θ d θ + ∫ cos 2 ⁡ θ - sin ⁡ θ d θ

Essa primeira integral é easy

- cos �� θ + ∫ cos 2 ⁡ θ - sin ⁡ θ d θ

Quanto a essa segunda, basta fazer uma mudança

cos ⁡ θ = t       →           d t = - sin ⁡ θ d θ

- cos ⁡ θ + ∫ t 2 d t = - cos ⁡ θ + t 3 3 =

Onde encontraremos como resultado final...

∫ sin 3 ⁡ θ d θ = - cos ⁡ θ + cos ⁡ θ 3 3 + C

Voltando para a integral

V o l u m e = 9 ∫ 0 π 2 sin 3 ⁡ θ d θ = 9 - cos ⁡ θ + cos ⁡ θ 3 3 0 π 2 =

substituindo...

9 - cos ⁡ π 2 + cos ⁡ π 2 3 3 - - cos ⁡ 0 + cos ⁡ 0 3 3 =

9 0 + 0 - - 1 + 1 3 = 9 1 - 1 3 =

6

Resposta

6

Exercícios de Livros Relacionados

Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.A parte da superfície z = 1 /
Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Utilize coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 1 + 2 x 2 + 2 y 2 e pelo plano z = 7 no primeiro octante
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Nos Exercícios 67 e 68, esboce a região de integração e o sólido cujo volume seja dado pela integral dupla.