Determine o volume do sólido dado.
e) Limitado pelos cilindros parabólicos , e pelos planos , . Dica: Determine o volume desse sólido por subtração de dois volumes.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume limitado pelos cilindros parabólicos , e pelos planos , . Nós sabemos que o volume é definido através da integral dupla:
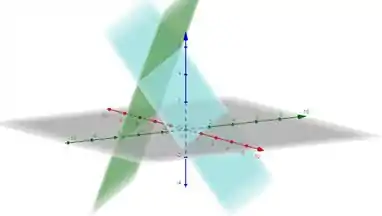
Só que nesse caso, nós temos duas funções para , que são os planos , . A gente pode ver eles no gráfico:
E a gente quer que eles sejam integrados dentro da região dos cilindros parabólicos , , que são esses aqui:
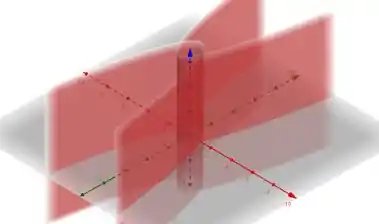
De ínicio isso pode parecer um pouco confuso, mas na prática o que nós vamos fazer é encontrar os limites de integração da integral dupla de e , usando as equações dos cilindros, e fazer , ou seja, como a subtração de dois volumes.
Vamos lá!
Passo 2
Vamos começar montando nossa integral, mas antes precisamos definir os intervalos de integração da região. Vamos fazer isso igualando as equações dos cilindros, para encontrar os pontos onde eles se interceptam:
Então, tá variando de a . E o tá variando entre um cilindro e outro, ou seja, . Com , temos nossa integral:
Integrando primeiro em relação a , temos:
Aplicando os limites de integração:
Agora integrando em relação a , temos:
E aplicando os limites de integração em :
Temos nosso volume:
Valeu, galera! Até a próxima! 😉