Calcule o volume do sólido que não contém a origem e é limitado pelas superfícies:

Temos um paraboloide, , limitado por um cilindro  e o plano .

Como ele quer a parte que não contem a origem, vamos ter esse pedaço aqui:

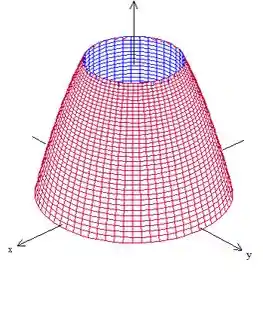
E a nossa função vai ser dada pelo próprio paraboloide  e o domínio vai ser a projeção disso, vamos ver como que vai ficar!

A projeção do paraboloide é dada quando e aí temos:

Mas temos aquele “furo” por causa do cilindro, que tem projeção de , então ficamos com algo assim:

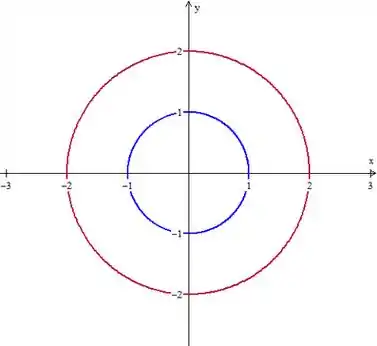
Que é muito bom de escrevermos em coordenadas polares, assim como nossa função

Vamos lembrar como que é a mudança para coordenadas polares:

Então aquela integral que a gente tem lá em cima fica:

Como vimos no passo anterior, o domínio é bem fácil de escrever em coordenadas polares. Temos, simplesmente e . Então:

Agora é só calcular a integral:

Pronto, tá feito!