Determine o volume do sólido que está sob o paraboloide , acima do plano e dentro do cilindro .

Como tanto a função que vamos integrar como a região de integração possuem termos e , vamos utilizar coordenadas polares. Faremos, então:

Agora que já definimos a substituição que faremos, vamos analisar os novos intervalos de integração.

O termo da equação da circunferência indica que ela não está centrada na origem. Vamos, então, completar o quadrado para descobrirmos seu centro:

Portanto, temos uma circunferência de raio centrada em , vamos representá-la graficamente:

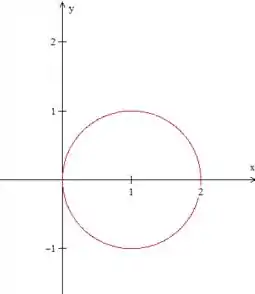
O ângulo varia entre e . Se não ficou claro a partir da imagem, pensa no seguinte: o ângulo deve cobrir toda a parte à direita o eixo , e cresce no sentido anti-horário, certo? Então, a partir da origem, o ângulo deve começar cobrindo a parte de baixo da curva, e seu valor inicial é . No ponto , vamos ter . Quando a curva começa a ser fechada na origem, vai se aproximando do valor .

Já , varia entre e a curva em vermelho, então, vamos substituir os valores que definimos para e na expressão do círculo:

Como sempre, teremos:

Vamos, então, montar a integral em coordenadas polares:

Vamos começar integrando em relação a :

Para integrar em relação a , vamos utilizar a fórmula do arco duplo:

Aplicando essa fórmula novamente: