Seja .
a) Esboce hachurando a região e ao lado a fronteira de .
b) Seja a integral dupla
Escreva na forma iterada, integrando primeiro em relação a e em seguida em relação a .
c) Escreva na forma da soma de duas integrais, integrando primeiro em relação a e depois a .
d) Agora, considere a integral dupla
em que . Calcule pelo método que preferir.
e) Determine, usando igualdades e desigualdades uma região que satisfaz as seguintes propriedades:
- A projeção da região no plano é a região plana definida no início da questão.
- O volume de é
Passo 1
a) Vamos lá, essa é bem direta! Basta pegar as desigualdades que formam e juntá-las!
Olhando pra primeira, temos:
Ela nos diz que, se estamos na curva , que é a parábola que tem a boca apontada para o sentido positivo do eixo e tem extremo na origem, então nossa região se encontra no interior dessa parábola! Andamos para o lado direito pois como é “maior ou igual”, andamos para o sentido do eixo :
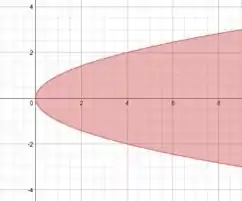
Beleza, primeira desigualdade concluída!
Passo 2
Vejamos a segunda:
Ela nos diz que, se temos a reta , então estamos do lado esquerdo da reta (pois, agora, ao contrário da parábola, o é “menor ou igual”!). Colocando essa região no nosso esboço fica:
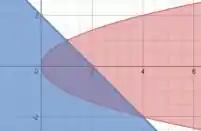
E, agora que você já está craque nisso, vamos colocar a terceira desigualdade no jogo! Ela é:
Ou seja, se temos a reta , então estamos abaixo dela, pois é menor ou igual a ela! Juntando no esboço que fizemos até agora, fica:

E, assim, a região é a confluência das três cores:
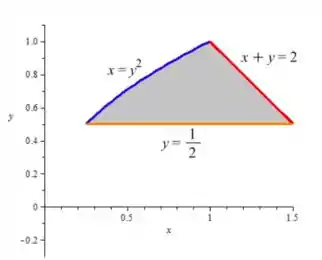
Aí está o esboço para ! Como pediram também o contorno da região, basta apagar o hachurado de dentro:
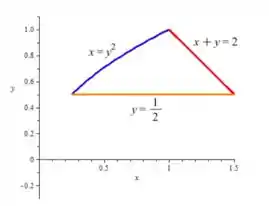
Passo 3
b) Agora estão nos pedindo para colocar os limites na integral dupla. Ok, como é pra integrar primeiro em relação a , então deve ser função de e, , por sua vez, deve estar entre duas constantes. Isso acontece quando olhamos as coisas na horizontal: estará entre a parábola é a reta, e estará entre e o pico de encontro dessas curvas!
Para a parábola, temos . Para a reta, temos . Assim, como está entre a parábola e a reta, vamos ter:
E, para o , temos que ver qual é o seu valor no encontro dessas curvas. Para isso, basta substituir uma na outra:
Então,
Resolvendo a equação , temos:
Para o nosso caso, , pois estamos vendo que a coisa toda ocorre sobre o eixo hehehe Colocando os limites do , teremos:
E é isso aí :D
Passo 4
c) Bão, agora é fazer exatamente a mesma coisa que o passo anterior, mas com a cabeça na vertical mesmo! Estamos com o entre duas constantes e o entre duas funções de .
Neste caso, perceba o seguinte: para estar entre duas funções, precisamos dividir a região entre duas etapas!
Veja, na parte do lado esquerdo, está entre a reta horizontal e a parábola:
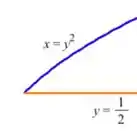
E, para essa parábola ser função de , precisamos isolar o :
E, assim, está entre e !
Agora, para a parte da direita, está entre essa reta horizontal e a outra
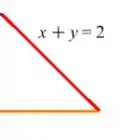
Transformando a reta vermelha em função de , teremos:
E, assim, está entre e !
Passo 5
Ok, agora que já temos os limites para o , vejamos entre que valores está o !
Olhando a figura como um todo novamente, temos:
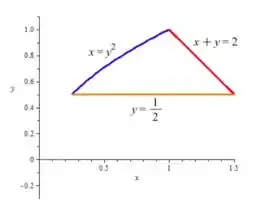
E, agora, precisamos descobrir as coordenadas de cada “vértice” de , pois são os pontos onde começam e terminam as duas etapas da divisão que fizemos!
O vértice do lado esquerdo acontece quando a equação da parábola encontra a reta , ou seja:
Pronto! Primeira coordenada de encontrada :D
O vértice de cima acontece quando a parábola encontra a reta vermelha, ou seja, quando , lembra? Colocando em qualquer uma dessas curvas, temos:
E vemos que a coordenada vale para esse encontro!
Finalmente, para o terceiro vértice, teremos o encontro da reta com a reta . Assim, a coordenada é:
Passo 6
Beleza, agora que temos os limites para e , basta montar a integral!
Para a parte da esquerda, está entre e , enquanto está entre e . Assim, nossa integral fica:
E, para a parte da direita, temos entre e , e entre e ! Colocando na integral, teremos:
E para a integral na região toda, temos:
Prontinho, letra detonada!
Passo 7
d) Vamos lá, firmeza que só faltam duas! Vamos tentar resolver aquela primeira que só tinha uma integral? Se ficar difícil tentamos essa soma de integrais que encontramos no passo anterior (mesmo que tenha mais integrais para resolver, pode ser que sejam integrais mais fáceis!).
Colocando a função pedida na integral, teremos:
Integrando em relação a , fica:
Colocando os limites, teremos:
E, agora, podemos dividir essa integral em duas, subtraindo uma da outra:
Passo 8
Vamos lá, para a primeira integral, temos:
Fazendo uma integração por partes, com e , e com e , teremos:
Resolvendo a integral de , teremos:
E fica:
Invertendo o sinal, teremos:
Passo 9
Para a segunda integral, teremos apenas que fazer uma substituição simples!
Colocando , teremos e os novos limites de integração serão e :
E fica:
E, juntando esse valor com o da outra integral, teremos:
Passo 10
e) Ultima letra! Vamo que vamo! Essa região que temos que descrever tem volume igual ao da integral dupla que acabamos de resolver né?
Os limites de integração dela formam exatamente a definição do , nossa região de integração. E essa região é a própria projeção em da região ! Com isso já matamos parte da descrição que temos que fazer de : É o conjunto dos pontos do em que e variam percorrendo a borda e o interior de !
E o que está faltando? Como estamos tratando de uma região do , temos que definir os limites das coordenadas , certo?! Mas, como sabemos que o volume de é o valor da integral dupla, então varia entre e a função que integramos, ! Portanto, fica:
E pronto, fechada a questão galera!
Resposta
a) Região: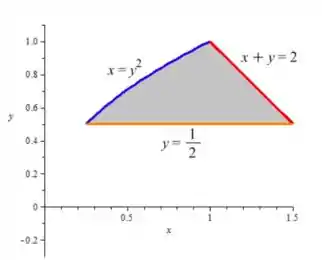
Contorno: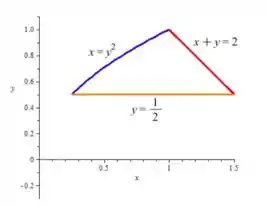
b)
c)
d)
e)