Calcule o volume do sólido delimitado pelo gráfico de:
Passo 1
Bom, antes de mais nada, vamos desenhar essa região do enunciado.
Obs: Tem uma superfície de equação meio esquisita aí, não é?
Não é necessário para essa questão que você saiba que superfície é essa, mas, a título de curiosidade, vamos mostrar aqui. Essa é uma cela, oblíqua aos eixos coordenados e :
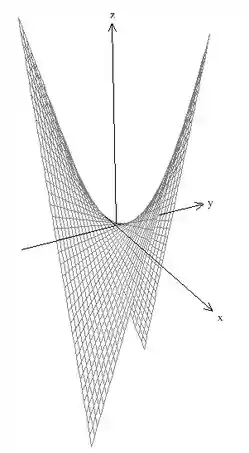
Se você não soubesse disso na questão não tinha problema nenhum, basta você entender que essa superfície limita a região “por cima” dela, já que é a única equação do enunciado em que a coordenada está presente. Bom, vamos lá.
Nós temos a superfície , que já vimos. Temos também , basta desenhar a reta no plano e alongar pelo eixo , formando um plano. Fazemos o mesmo para os planos e .
Temos então a seguinte região:
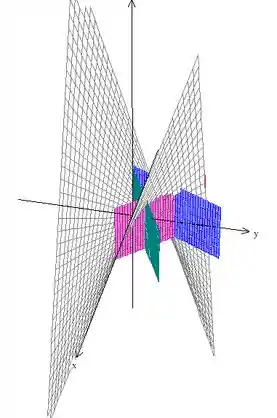
Outro ângulo, para você visualizar melhor:
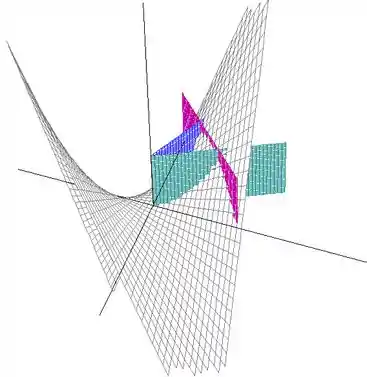
Beleza? Como o problema não menciona nenhum plano fechando a região por baixo, vamos assumir que , ou seja, que o volume é limitado pelo plano . Agora, chamando de essa região que acabamos de analisar, o problema pede então .
Passo 2
Certo, agora precisamos escrever matematicamente essa região, ok? Vemos que, na coordenada ela é limitada por duas funções ( e ) e no plano , por uma área, que chamaremos de .
Sendo assim, esse volume pode ser escrito da seguinte forma:
Passo 3
Agora precisamos escrever matematicamente essa área , como em qualquer integral dupla que já fizemos. Imagine o sólido visto de cima, temos isso aqui:
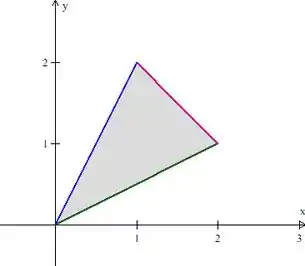
Essa é a área que limita no plano . Vamos descrevê-la como uma região do tipo I, na coordenada ela é limitada por funções e na coordenada é limitada por números. Aqui não tem jeito, precisamos dividir essa região em duas, a da esquerda com e a da direita com . Vamos chamá-las de e , .
A região da esquerda é limitada na coordenada pela reta verde e pela azul , enquanto a da esquerda é limitada pela reta roxa e pela verde .
Podemos então escrever o seguinte:
Passo 4
Agora vamos substituir na integral esses intervalos que encontramos:
Cuidado com a ordem dos diferenciais! Ela tem que acompanhar os intervalos da integrais.
Passo 5
Agora em relação a :
Passo 6
Finalmente, em relação a :