Calcule o volume do sólido que é delimitado pelo paraboloide elíptico , pelos planos e e pelos planos coordenados.
Passo 1
Para entender o que está sendo pedido, vamos fazer um esboço. Esse seria o paraboloide que o enunciado menciona, vamos primeiro desenhar esse paraboloide:
Repara que a sua equação é
Então o vértice desse paraboloide está no , vai ficar como na figura de baixo.
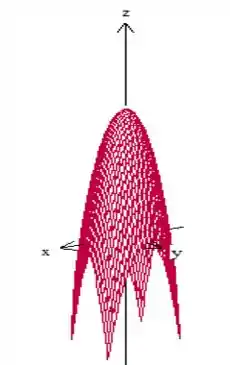
Mas o problema diz que a superfície é cortada pelos planos coordenados ( , e ) e também pelos planos e , certo? Faremos isso. Vamos manter o paraboloide limitado com
O gráfico vai ficar
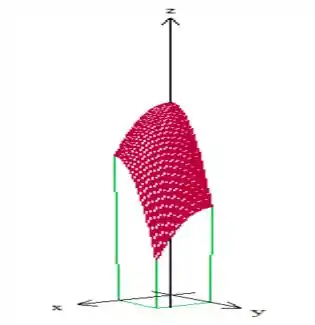
Pronto, é o volume dessa região que a questão pede (uma caixa com a parte de cima curva).
Passo 2
Agora devemos montar o problema em linguagem matemática. Para isso, basta você se lembrar da definição de Integrais Duplas. Integrar uma função em uma região do plano não é equivalente a calcular o volume entre essa superfície e esse plano? Então é isso que faremos.
Vamos escrever a equação do paraboloide em função de e Basta isolar o :
Note que, como os coeficientes de e de ficaram negativos, o paraboloide está virado para baixo. Nunca teremos um valor de maior que (quando e são iguais a zero).
Montaremos, então, a integral:
Passo 3
Para calcularmos essa integral dupla, vamos separá-la em integrais simples:
Devemos, então, encontrar os valores dos limites de integração , , , e . Repare que a região formada no plano ,abaixo do pedaço que restou do paraboloide, é um retângulo que pode ser escrito assim:
Pois tanto como variam entre e . Basta, agora, escrever esses números na integral:
Passo 4
Vamos começar integrando em (a integral de dentro):
Passo 5
Agora, vamos integrar em :