- Calcule o volume do sólido interior à esfera e ao cilindro e acima do plano .
Passo 1
Pow! O problema nos pediu um volume de sólido, e a essa altura, podemos calcular um volume utilizando uma...
Mas veja que para resolver essa integral aí necessitamos de algumas informações:
- Quem é o ?
- Quem é a região de integração ?
- Quem é o ?
- Quem é a região de integração ?
Para ambas as perguntas, vamos encontrar as respostas no esboço do sólido no espaço. Bora?
Passo 2
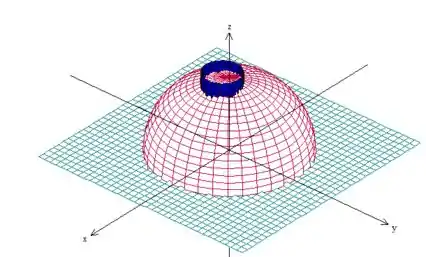
Pois bem! O sólido que estamos trabalhando está delimitado pela esfera
Essa é uma esfera normal e de raio :
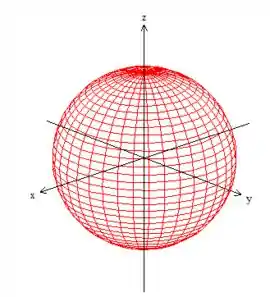
Mas não queremos toda a esfera, por isso o problema nos limita a esfera pelo plano , ou melhor, o próprio plano
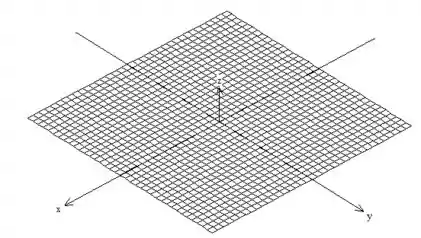
Passo 3
Contudo, ainda não terminamos de encontrar o sólido, afinal de contas existe um cilindro que delimita essa região.
Porém esse cilindro não é como estamos acostumados, ao redor do bonitinho,
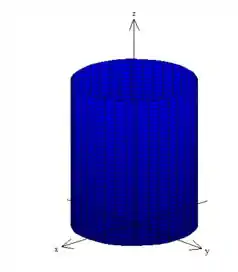
ele é um cilindro deslocado, quer ver só?!
Passa esse pro outro lado...
Esse termo aparece se fizermos . Mas pra fazermos isso temos que colocar na equação e tirarmos ao mesmo tempo (para não alterar a expressão)
Olha que bacana! Agora podemos...
RA! É de fato um cilindro de raio muito parecido com o de cima, mas ele está deslocado unidades em
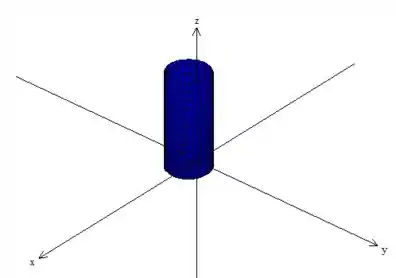
Assim, o sólido que queremos está dentro desse cilindro deslocado
Passo 4
Agora já conseguimos juntos aqui responder a primeira pergunta:
Afinal de contas você já sabe que essa função aí é a função que representa a superfície “teto” do sólido, certo?
E quem é essa superfície?
Exato! O pedacinho de esfera ;)
Como a esfera tem essa equação aqui , precisamos mexer um pouquinho nela a transformando nessa função de e , bastando isolar o no caso...
como o teto esta em cima...
Passo 5
Quanto a essa pergunta aqui...
como e são as variáveis principais, devemos encontrar essa região na “sombra” do sólido no plano .
Olhando então apenas para essa sombra de cima pra baixo obtemos...
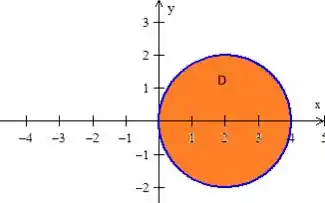
As variáveis e estão aí dentro
Passo 6
Pow! Estamos trabalhando com uma região circular, ou seja, vamos utilizar as coordenadas polares:
Uma equação que nos ajuda muito é a equação da circunferência...
E, claro, o Jacobiano:
Passo 7
Mas como você já sabe, nunca podemos sair das mudanças sem dizer onde os novos caras, e no caso, estão variando.
Tenha bem em mente quem é a região :
O é o ângulo que varia nessa região saindo do eixo , dessa forma
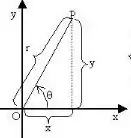
Pra ele começar varrendo lá de baixo, devemos ter
Quanto, ao raio, se você notar, ele varia de até a circunferência azul
Como a circunferência azul tem equação do cilindro no plano , , basta substituir as polares
Logo
Passo 8
Nessa mudança é fundamental não se esquecer de trocar a função que estamos trabalhando pelas novas coordenadas:
substituindo...
não se esqueça de multiplicar pelo , heim!
Logo essa é a função que estamos trabalhando agora
Passo 9
Montando a integral, agora, com todos os dois dados principais:
Resolvendo primeiro a integral de dentro...
Pow! Essa integral de dentro aí pode ser resolvida caso façamos uma troca:
antes de substituirmos, não esqueça de trocar os limites também
integrando...
Sabendo que , podemos simplificar
A primeira integral é fácil, afinal é uma constante ali dentro
Quanto a essa segunda integral aí, tome cuidado! Pois:
Logo temos que separar essa integral uma pros negativos e outra pros positivos, veja
Mas não se preocupe que apenas precisaremos calcular uma integral, afinal anota esse bizu:
Quando temos uma integral em um intervalo simétrico e, além disso, a função é a mesma com a única diferença que ela tem um sinal no lado positivo e outro no lado negativo, então
Assim
Bora calcular essa integral? (vamos trabalhar com ela indefinida aqui apenas para não atrapalhar o raciocínio):
Como o coeficiente do seno é impar, podemos separar dessa forma
onde lembrando que ...
Essa primeira integral é easy
Quanto a essa segunda, basta fazer uma mudança
Onde encontraremos como resultado final...
Voltando para a integral