Considere a região espacial
Onde é a região plana descrita na questão .
- Expresse o volume de como uma soma de integrais iteradas nas variáveis cartesianas e , integrando primeiro em relação a e em seguida com respeito a . (Obs.: Neste item não é pedido o cálculo da integral)
- Expresse o volume de como uma soma de integrais iteradas nas variáveis cartesianas e , integrando primeiro em relação a e em seguida com respeito a . (Obs.: Neste item não é pedido o cálculo da integral)
- Calcule o volume de (usando o método que preferir)
OBS: faça essa questão depois de dar uma olhada na primeira questão dessa prova, elas tem relação.
Passo 1
Primeiro vamos relembrar a região
Com
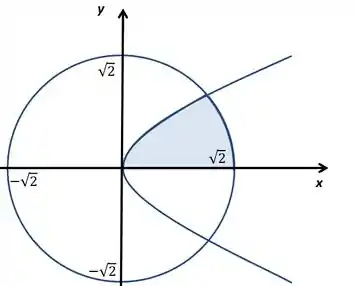
Já vimos também que o ponto de encontro entre a parábola e a circunferência é o ponto
O volume vai ser
Passo 2
Para escrevermos a integral da forma que ele quer vamos precisar escrever como a soma de duas integrais. Isso porque uma parte da figura, o valor de , vai de até a parábola, e em outra parte ele vai de até a circunferência.
Vamos fazer a primeira parte, onde , vai de até a parábola,
O valor de vai ser
Enquanto vai ser
E o limite maior vai ser
Sendo positivo porque temos
Então a primeira região, , vai ser
Passo 3
A segunda parte vai ter o valor de indo de até a circunferência,
O limite maior vai ser
Isso, de novo, porque
Os valores de vão de até o fim da circunferência, no caso,
Então a segunda região, , vai ser
Passo 4
A integral vai ficar
Passo 5
Já vimos na questão que a região vai ser
Então a integral vai ficar
Passo 6
A integral que achamos no final do passo é mais fácil, isso porque integral é levemente tranquilo rs. Vamos usar essa integral
Vamos usar um pouco de álgebra nesse fração
Se imaginarmos a parte de cima é
Fazendo as raízes, vamos achar , e a fatoração fica
Trocando por
Fatorando mais um pouquinho
Deixando a fração assim
A integral vai ficar