Considere a região do espaço
- Considere a região do plano Considere Fr(R), a fronteira de R.
- Calcule o volume de .
Desenhe R, explicitando na figura os dois pontos da fronteira Fr(R) que pertencem ao eixo z.
Passo 1
Para começar essas questão, vamos ver a planificação no plano yz. Para isso, faremos x=0
Além disso temos ainda o plano z=2.
Ficamos então com:
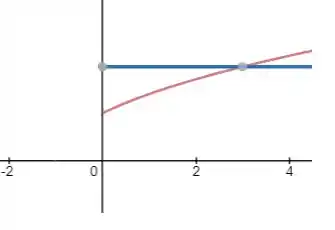
Os pontos que pertencem ao eixo z serão então:
O segundo ponto será aquele da função de baixo (vermelha) tem y=o
Logo:
Logo:
Passo 2
Na letra B ele nos pede para calcular o volume. Bom, vamos então montar a integral, fazendo uma mudança de coordenadas, onde:
Quando vista debaixo, a região que estamos trabalhando é essa:
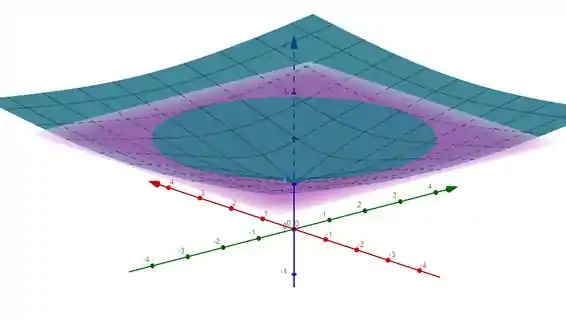
Observe então que o z varia entre a função debaixo e a de cima (2).
Para descobrir a variação de , percebemos que varia entre 0 e 2, enquanto para r, substituímos na equação.
Observe que temos o r máximo quando z=2. Logo:
Passo 3
Nosso próximo passo será então montar a integral (sem esquecer de escrever o campo em função das novas coordenadas e do jacobiano).
Resolvendo primeiro a integral de dentro ficamos com:
Fazendo uma substituição simples:
Trazendo o restante da integral de volta: