2) Considere as regiões do espaço
e
- Identifique as fronteiras de e , esboçando lado a lado as duas superfícies clássicas.
- Considere .
- Escreva a integral dupla
- Escreva o volume de na forma
- Calcule , onde é a integral do item .
Seja . Desenhe hachurando e desenhe ao lado a fronteira de (observe que está contida no plano , ou seja, no plano ).
na forma de uma integral iterada, integrando primeiro com respeito a e depois com respeito a (Obs.: é a região planado item ).
Neste item não é necessário encontrar o valor numérico de .
explicitando , e .
Neste item não é necessário encontrar o valor numérico de .
Passo 1
Pow, quando um problema te pede para identificar fronteiras assim, já tenha em mente que ele não vai te dar nada muito mirabolante que você não tenha visto. São superfícies conhecidas. No nosso caso mesmo, a primeira , veja de passarmos o para o outro lado...
Pegando só a igualdade, pois queremos a superfície...
HAHA! É a equação de um hiperboloide de uma folha:
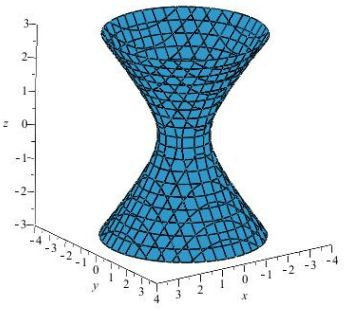
Não esquenta com esse maior ou igual. Isso só significa que estamos trabalhando com a região do lado de fora dele ;)
Passo 2
Vejamos o outro, ...
Colocando a igualdade...
Outra superfície bem legal, o paraboloide! Mas nesse caso, o paraboloide está deslocado uma unidade em para baixo...
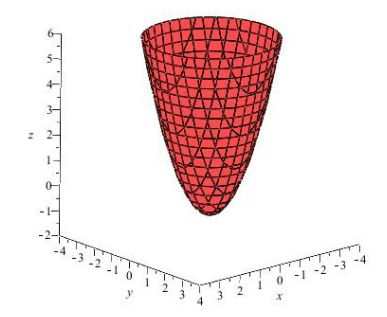
O sinal de maior significa que a região, deve estar no interior dele.
Passo 3
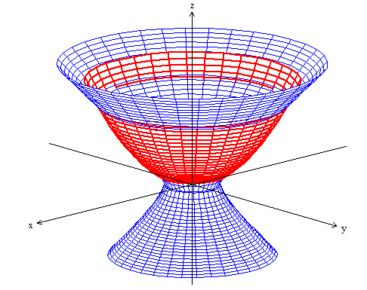
Bem, conforme o item nos pede, devemos colocar essas superfícies delimitadoras lado a lado:
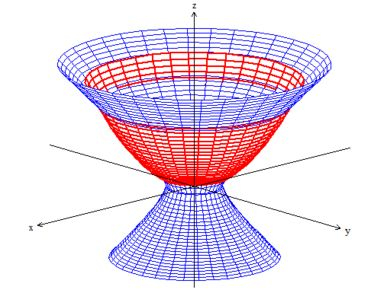
Note que ambas juntas, delimitam uma região que está exatamente dentro do paraboloide e fora do hiperboloide. Exatamente como queríamos pelos sinais de maior e menor saca?
Passo 4
Pela própria observação do enunciado:
“observe que está contida no plano , ou seja, no plano ”
O que queremos é seccionar, ou melhor, “cortar” a região do passo anterior, por um plano , e observar, o corte nesse plano:
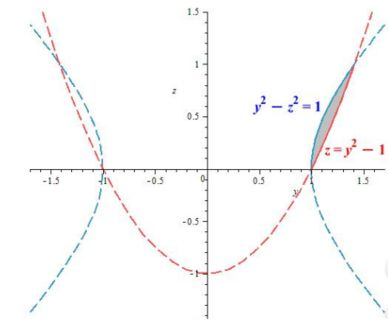
Repare que existem, duas regiões do interior delimitado pelas duas superfícies. Porém, como o enunciado nos pediu, apenas queremos a parte com maior que . Por isso, a rachuramos ;)
Passo 5
Antes de passarmos ao próximo enunciado, acho que te devo uma explicação:
Você pode estar se perguntando: “de onde veio aquelas equações de curva?”
Bem, o que fizemos é pegar a parte do sólido no espaço que está delimitado por duas equações...
E corta-los pelo plano ... Logo...
Ambas no plano , saca? A parábola está deslocada unidade em , e a hipérbole tem como vértice o e também.
Passo 6
Epa! Agora necessitamos de escrever uma integral iterada
Mas invertendo essa ordem aí, ou seja, primeiro em e depois . Precisamos de quê? Descrever a região . Como queremos o depois, ele deve ter os limites numéricos, enquanto que o , deve variar entre funções.
Bem, para ter essa configuração, configuração de reta do , antes precisamos encontrar os pontos que elas se cruzam...
Substituindo o na equação de baixo...
Como o nosso foco é encontrar o como um intervalo numérico, vamos substituir esses valores na primeira equação...
Era para ser , mas como estamos no lado direito...
Então, já descobrimos a variação de ...
Passo 7
Ainda nos falta a variação de dentro da região. Bem, se você notar...
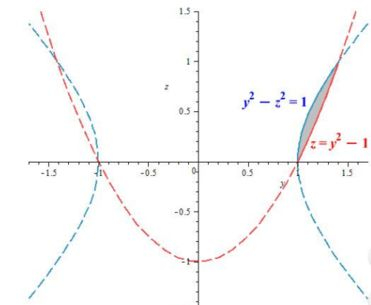
entra na parábola vermelha, e sai na hipérbole...
A equação da hipérbole é um pouco mais chatinha, pois temos ...
Extraindo a raiz e pegando o lado maior que ...
Passo 8
Com a informação desses dois intervalos...
Montando a integral iterada...
Calculando a primeira integral, de dentro...
Passo 9
Temos que encontrar agora uma expressão que calcule o volume do sólido...
A essa altura do campeonato, o volume é calculado por uma integral dupla:
Ou seja, é uma integral dupla na região de projeção do sólido no plano de uma subtração de funções por . Bora encontrar esses caras?
Passo 10
Vamos começar com a subtração de funções. Bem, a função de cima, , é uma função que representa a superfície de cima. No caso, essa superfície, como pode ver no esboço... é o hiperboloide...
A função que estar por baixo, vamos tirar da outra superfície... A que está por baixo... O paraboloide:
Então...
Passo 11
A região , não é a mesma região encontrada acima (até porque essa daqui é e não ). A , vamos encontrar fazendo uma a intercessão das duas superfícies no espaço...
Isolando o no primeiro e substituindo na de baixo...
Substituindo na primeira equação...
Ou seja, o e , variam no interior dessas duas circunferências:
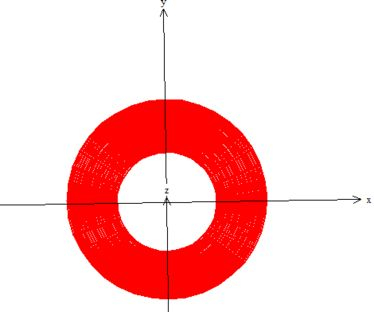
Já era de se esperar neh, pois a região inteira é circular em torno de :D!
Passo 12
Bem, se estamos em uma região circular, coordenadas polares é uma boa:
E uma equação que ajuda muito é a equação da circunferência...
Os limites de e se resolve vendo o esboço da região ...
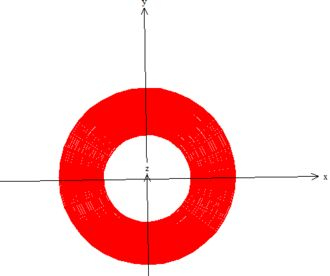
Repare que dá uma volta completa ao redor da origem...
Enquanto que o raio, varia do raio menor até o maior que vimos ser ...
Passo 13
Voltando para a integral...
E substituindo tudo não se esquecendo do Jacobiano...
Como o enunciado pediu que comparássemos...
Passo 14
Calculando...
Passando esse para fora...
Cara, essa integral é mesma coisa kkkk. Só muda o nome da variável de para , o que é totalmente permitido em integrais. logo...