Considere o sólido
- Faça um esboço de .
- Calcule o volume de .
Passo 1
Letra a)
Vamos por partes. Nós temos as seguintes superfícies limitando nossa região;
Nós sabemos que é um paraboloide virado para baixo com simetria em e ponto mais alto em . As superfícies e são planos perpendiculares ao plano , são como retas e repetidas ao longo do eixo . Vamos desenhar isso aí então:
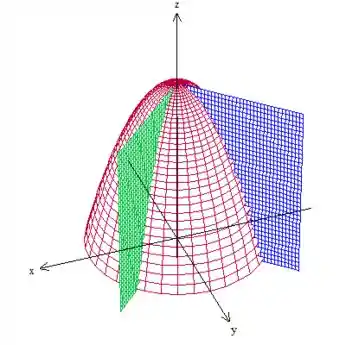
Certo, agora temos que considerar que e . Fazendo esses cortes, vemos que o sólido que sobra é esse aqui:
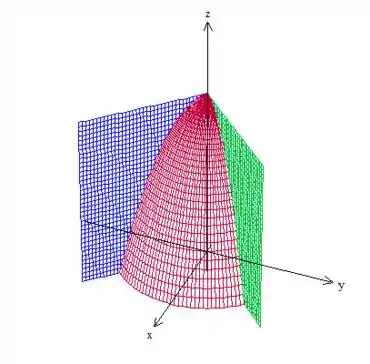
Passo 2
Letra b)
Agora vamos calcular o volume desse sólido.
Como podemos ver, no plano , temos um domínio . Em , o sólido é limitado em cima pelo paraboloide e embaixo pelo plano .
Então, a função que vamos integrar será , em cima da região definida no plano .
Passo 3
Agora precisamos descrever esse domínio . Para isso, vamos ver projeção do sólido plano :
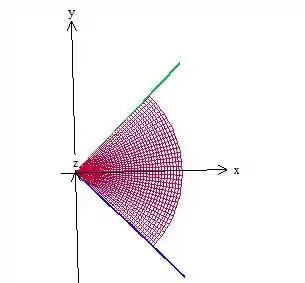
Fazendo a interseção do paraboloide com o plano , temos:
Uma circunferência, como podemos ver na figura acima. Na verdade, é um setor, limidado pelas retas e (que são os planos vistos de cima).
Como se trata de uma circunferência, vamos escrevê-la com coordenadas polares:
O raio vai desde na origem até a circunferência, onde . O intervalo de temos que descobrir fazendo a mudança polar na equação dos planos. Na verdade, nem precisamos né, sabemos faz ângulo de com o eixo . Então temos:
Isso também vai alterar a função que estamos integrando! Se liga:
Passo 4
Podemos agora montar a integral, sem esquecer do Jacobiano:
Agora é só resolver e partir pro abraço!