Seja a região do espaço definida por
Seja
- Esboce a fronteira de e no mesmo desenho esboce , hachurando .
- Calcule o volume de .
Passo 1
Letra a)
Vamos lá galera, essa região é bem estranha né? O limite inferior é até tranquilo de entender, simplesmente , que é um plano paralelo a . Agora, o limite superior vamos ter que tomar mais cuidado, beleza?
Antes de mais nada, vamos escrever aqui a função que temos que esboçar
Primeira observação é que o expoente “” é sempre positivo, com isso o denominador
Sabemos então que
E portanto, como esse termo do meio é igual a , os seus limites seriam
Mas o enunciado lá em cima diz que , lembra? Então seus limites são
Beleza, já sabemos que varia num intervalo pequeno, mas como vamos fazer o esboço dessa função bizarra? Vamos ter que fazer uma mudança de variáveis aqui pra facilitar nossa vida! Note que temos o termo ali né? Quando esse cara aparece geralmente vamos fazer uma mudança polar, assim
Dessa forma
Vamos tentar reorganizar isso ai
Perceba agora que, para cada valor de z, vamos ter um raio associado! Por exemplo,
Já começamos a ter uma ideia da função no plano né?
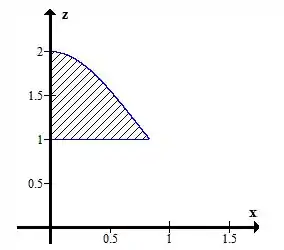
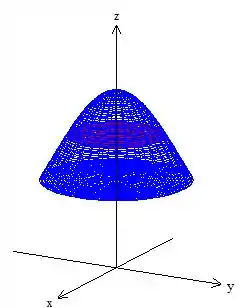
Como fizemos tudo isso em coordenadas cilíndricas, só precisamos rotacionar essa superfície em torno do eixo para gerar nosso sólido! Fica assim
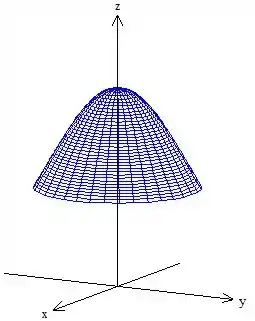
Passo 2
Temos já a fronteira de , só que, além disso, o enunciado te pede pra desenhar uma região que é a interseção desse sólido com o plano . É exatamente isso que precisamos fazer! Simplesmente desenhar um plano cortando esse sólido e marcar a região .
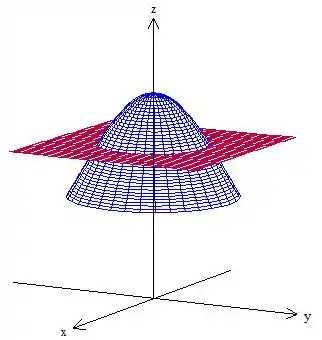
A região vai ser interior ao sólido, fica assim o esboço final
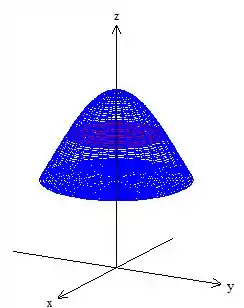
Passo 3
Letra b)
Vamos calcular o volume agora né? Sabemos que os limites inferiores e superiores de são esses aqui
Portanto, para calcularmos esse volume, precisamos calcular a seguinte integral
Beleza, e como fazemos isso? Precisamos projetar esse sólido no plano , achar os limites de integração e, por fim, calcular a integral.
E quem vai ser essa região ? Bom, como o nosso sólido foi obtido rotacionando uma superfície, nada mais justo que no plano aparecer um círculo! Até porque fizemos uma mudança polar, lembra?
E quais vão ser os limites de ? Isolamos nessa função lá no passo 1, ficou assim
Graficamente, vemos que o menor raio do nosso sólido aparece quando e, por outro lado, o maior raio aparece quando , não é? Portanto
Passo 4
Pronto, encontramos os limites! Vamos substituir tudo na integral
Passo 5
Para integrar em , vamos dividir em duas integrais:
Para resolver a primeira, precisamos fazer uma mudança de variável
Reescrevendo fica assim
Aqui, é valido lembra da propriedade de logaritmo neperiano que diz que
Portanto
Passo 6
A segunda integral e mais facilmente calculada
Passo 7
O volume de vai ser
Resposta
a)
b)