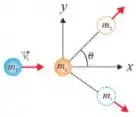
Q - Uma partícula de massa se movimenta com velocidade e colide elasticamente com uma partícula em repouso de massa como mostrado na figura. Após a colisão, é observado que as duas partículas têm mesma componente dos vetores velocidade. Determine o módulo do vetor velocidade da partícula de massa , em , imediatamente após a colisão.
Passo 1
Vamos resolver essa juntos? Então vamos!
Para encontrar o módulo do vetor velocidade de vamos usar a conservação de momento do sistema e ainda se for preciso a conservação de energia já que a colisão foi elástica.
O momento inicial (antes da colisão) só é composto pelo o momento de , já que está em repouso, já o momento final tem contribuição das duas partículas, então temos o seguinte:
Vamos dá uma cara para os vetores das velocidades finais, para melhorar a cara dessa equação e para facilitar nossa vida na hora de usar a conservação de energia, já que lá precisamos dos módulos das velocidades.
Passo 2
Usando essas expressões do final do passo e as expressões das massas a equação do momento fica da seguinte forma:
Disso tiramos que:
E segundo o enunciado temos que as componentes das duas massas são iguais, logo:
Logo temos que:
E da segunda equação, referente a direção , temos:
Passo 3
Agora falta encontrar uma expressão melhor para , para isso vamos usar a conservação da energia cinética, temos o seguinte:
Su8bstituindo com as expressões que conhecemos, temos:
Com isso, temos que:
Assim temos que:
Mas se olharmos a figura vemos que a bola foi para direção positiva de , logo o valor que nos interessa é o positivo.
Com esse resultado que chegamos vemos que:
Passo 4
Agora podemos montar o vetor , temos:
Agora vamos calcular o módulo que o enunciado quer saber.
Logo temos que:
E está feito o que o problema queria!