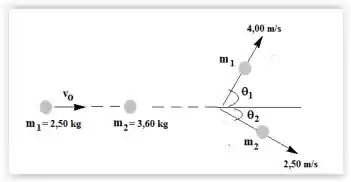
Dois objetos se encontram sobre uma superfície horizontal sem atrito. Um objeto de 2,50 kg de massa colide elasticamente com outro de 3,60 kg que, inicialmente, está em repouso. O objeto mais leve possui, após a colisão, uma rapidez de 4,00 m/s e se move formando um ângulo em relação à sua direção original; o objeto mais pesado possui uma rapidez de 2,50 m/s e se move formando um ângulo , conforme é mostrado na figura.

(a) Explique se o momento do objeto mais leve se conserva ou não.

(b) Determine a rapidez inicial do objeto mais leve.

(c) Calcule os ângulos e

Vamos determinar agora o pedido pelo item (b): a velocidade inicial do objeto mais leve.

Sabemos que a colisão ocorre num sistema isolado e, portanto, o momento total desse sistema, que é formado pelos dois objetos, se conserva:

Sabemos também que a colisão é elástica e isso significa que a energia cinética do sistema se

conserva. Assim, podemos montar, lembrando que a velocidade inicial do objeto 2 é nula:

Como temos:

Podemos manipular essa equação e descobrir :

No item (c), são pedidos os valores dos ângulos e :

Podemos enunciar novamente a equação da conservação do momento linear do sistema:

Como temos componentes das velocidades finais tanto no eixo x quanto no eixo y, podemos escrever a equação de conservação do momento linear para cada eixo:

Para o eixo x, temos:

Para o eixo y, temos:

Vamos manipular essas duas equações montadas para cada eixo a fim de descobrirmos os valores dos ângulos:

Da equação do eixo x, podemos escrever:

Da equação do eixo y, podemos escrever:

Agora, vem uma parte mais chatinha. Vamos elevar ao quadrado as duas equações e soma-las.

Mas, por que isso?

Porque temos aquela identidade antiga de

E colocando ao quadrado, temos grandes chances de utiliza-la.

Show!

Vamos lá!

Colocamos ao quadrado cada equação e, em seguida, somamos:

Show! Agora que somamos, viu a utilidade do quadrado?

Podemos aplicar a identidade e deixar a equação bem mais simples:

Agora temos uma única incógnita, o . Podemos manipular:

Como já temos todos esses valores:

Podemos substituir:

Só falta acharmos agora:

Uma boa saída é voltarmos com a equação:

Manipulando:

Sabemos que

Substituindo os valores, chegamos a:

Ufa! Essa questão era realmente cansativa!