Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
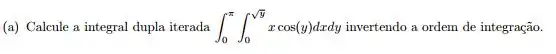
Passo 1
Como o enunciado já falou direto, a gente vai ter que inverter essa ordem de integração. Lembra como a gente faz isso? Não pode esquecer! A gente tem que esboçar a região, sempre.
Temos nesse caso aqui, pelas integrais:
Esse é o mais complicadinho, né? Mas ele veio da parábola
Então o esboço fica assim:
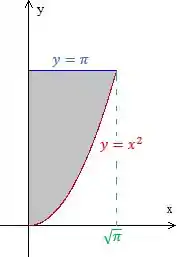
Passo 2
Vamos fazer agora a análise pelo e pelo . Lembrando que no a gente fica com isso aqui
E no a gente fica com
Ou seja, o enunciado deu pra gente o , então queremos inverter tudo para o .
No esboço do , a gente analisa a região com setas verticais, e no a gente analisa com setas horizontais, assim:
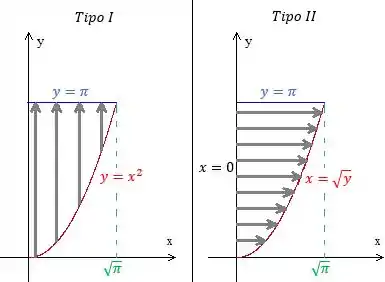
Analisando o Tipo I, a seta sempre entra na parábola e sai na reta , tudo isso no intervalo de entre e . Portanto
Passo 3
A integral fica assim então
Integrando em
Como , temos que
Passo 4
Para integrar em , vamos ter que fazer uma substituição simples:
Integrando em