Calcule .

Bom, olhando para a integral, já vemos que tá complicado integrar isso aí direto. Digo, em relação a tá complicado, mas em seria bem melhor, não é? Vamos tentar trocar essa ordem de integração então.

Queremos isso aqui:

Ou seja, precisamos reescrever essa região de integração, para isso, vamos fazer um desenho dela, ok?

Vemos que varia desde até a reta . Mas que diabos de curva é ? Repara no seguinte:

Até aqui nada mudou, certo? Agora vamos elevar os dois lados ao quadrado:

Como elevamos ao quadrado, temos que levar com a gente a restrição:

Isso porque a raiz tem que ser , como temos um sinal negativo antes dela, sabemos que o lado esquerdo da equação é . Cuidado porque essa informação se perde quando elevamos os dois lados da equação ao quadrado! Por isso, temos que fazer essa análise.

Rearrumando a equação, temos:

Com . Ok, agora vamos pensar.

Se fosse , seria uma circunferência de raio centrada na origem. Esse ao lado do faz com que essa circunferência tenha o centro deslocado em , no caso, para . Ou seja, isso aqui:

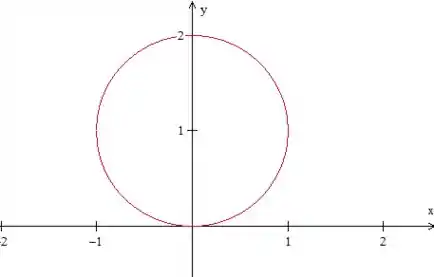
Calma que tem mais. Não podemos nos esquecer de que :

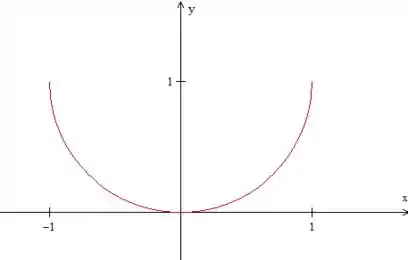
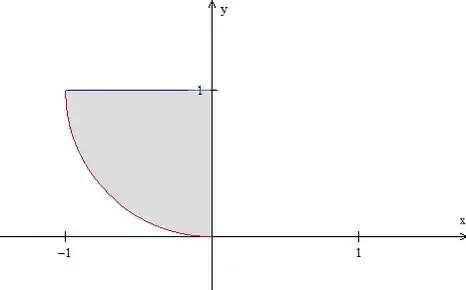
Tá, isso aí representa a curva . Sabemos que a região tem desde essa curva até a reta .

Além disso, os limites lá da integral inicial eram:

Portanto vai desde até .

Temos, então: