Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 66123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646567686970717273747576777879808182838485868788899091929394

Enunciado

UFMG – Cálculo 3 – Lista 1 – Questão 4

Calcule a integral trocando a ordem de integração

∫ 0 1 ∫ 2 x 2 y 2 sin ⁡ ( 2 π x y ) d y d x

Passo 1

Oi pessoal, tudo bem? Vamos começar?

O problema começa nos dando essa integral iterada

∫ 0 1 ∫ 2 x 2 y 2 sin ⁡ ( 2 π x y ) d y d x

E pediu para invertermos os limites de integração antes de integrar! e agora, o que fazer? Nossa pergunta de milhões precisa de uma resposta de milhões...

Fazendo um desenho da região! Pegando os limites de integração vemos que

2 x ≤ y ≤ 2

0 ≤ x ≤ 1

E esboçando essa região, temos isso aqui

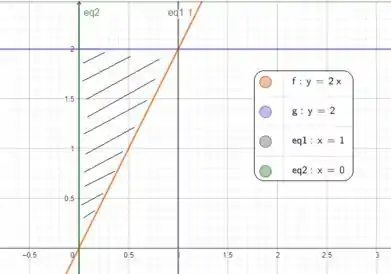
x = y / 2 , então esse é nosso limite superior em x . E a função mais à esquerda é x = 0 . Já os limites em y vão de 0 até 2

Invertendo a ordem temos o seguinte

0 < x < y / 2

0 < y < 2

Daí nossa integração começa em x !

d x   d y

E o integrando? Fica igual! Só mudamos a ordem de integração! Beleza?

Agora é #partiu integrar!

Mas relaxa, vou fazer passo a passo com você!

Passo 2

A integral que precisamos resolver é essa

∫ 0 1 ∫ 2 x 2 y 2 sin ⁡ ( 2 π x y ) d y d x

Mudando os limites de integração temos

0 ≤ x ≤ y / 2

0 ≤ y ≤ 2

∫ 0 2 ∫ 0 y / 2 y 2 sin ⁡ ( 2 π x y ) d x d y

Beleza?

Agora nossa missão é resolver essa integral!

Passo 3

Nossa integral é essa aqui

∫ 0 2 ∫ 0 y / 2 y 2 sin ⁡ ( 2 π x y ) d x d y

Considerando y constante, e fazendo a substituição simples de

u = 2 π x y

d u = 2 π y   d x → d u 2 π y = d x

Quando x = 0 → u = 0 , quando x = y 2 → u = π y 2 . Integrando e substituindo os limites temos:

∫ 0 2 y 2 2 π y - cos ⁡ u 0 π y 2 d y = 1 2 π ∫ 0 2 y   cos ⁡ π y 2 + 1 d y =

1 2 π ∫ 0 2 y cos ⁡ π y 2 d y + 1 2 π ∫ 0 2 y   d y

Tudo bem até aqui?

Agora vamos resolver essas duas integrais em y !

Passo 4

A mais à esquerda é por substituição simples e a outra por integração direta. Beleza? Assim temos:

u = π y 2 → d u = 2 π y   d y → d u 2 π = y   d y

Quando y = 0 → u = 0 , agora quando y = 2 ,   u = 4 π . Integrando temos:

1 2 π ∫ 0 2 y cos ⁡ π y 2 d y + 1 2 π ∫ 0 2 y   d y

1 2 π ∫ 0 4 π cos ⁡ u d u 2 π + 1 2 π y 2 2 0 2 = 1 2 π s e n   u 0 4 π + 1 2 π y 2 2 0 2

Agora é só aplicar os limites de integração!

1 2 π s e n   4 π - s e n   0 + 1 2 π 4 2 - 0 = 1 π

Beleza? Espero ter ajudado!

Até a próxima!

Resposta

1 π

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.