Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Resolva a integral dupla
Desenhe a região de integração.
Passo 1
Primeiro de tudo, vamos lembrar que a função é ímpossivel de integrar em direto, mas esse é um caso clássico de inversão de ordem de integração, vamos tentar!
O enunciado mesmo pede pra desenharmos a região de integração e esse é o primeiro passo pra tentarmos entender melhor como que ficará nosso integral com a ordem invertida.
Temos uma região tipo , com e o variando entre uma reta e uma constante , que graficamente fica assim:
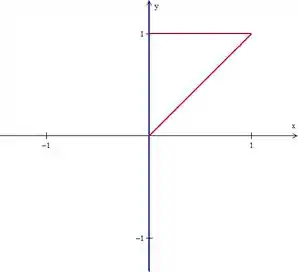
Que também é uma região do tipo com e variando de a .
Passo 2
Então, nossa integral vai ficar:
Que a gente integra primeiro em :
Passo 3
E agora em , que a gente consegue resolver pela substiuição:
Então a gente fica com:
E aplicando os limites de integração:
Pronto, com esse macete ficou bem mais tranquilo, viu?