Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Questão 1: Calcule a integral iterada abaixo:
Passo 1
Pow, em uma integral dupla que está já na sua forma iterada, podemos começar tentando resolver a integral de dentro como manda o “figurino”:
EPA!!! Olha a pegadinha do malandro aí (tava bem fácil pra ser verdade, neh?)! Essa integral de dentro aí em , por mais que tentamos, não vamos conseguir resolve-la com as técnicas de integração que conhecemos: substituição, por partes... Nada disso funciona com ela .
“Então e agora? O que fazemos?”
Calma Jovem! Quando isso acontece é porque o seu professor quer saber se você sabe uma coisa: realizar uma inversão da ordem de integração. Então vamos lá?
Passo 2
Pois bem, em problemas como esse, troca de ordem de integração, devemos sempre começar fazendo um esboço da região. Para fazermos isso, você terá que retirar da integral, duas informações maravilhosas que são o intervalo de (que no caso é o intervalo de fora):
e o intervalo de :
OBS. IMPORTANTE: Pow! Repare que com o variando em um intervalo numérico bem definido e o entre funções, isso nos configura uma região do tipo II e o que devemos fazer é basicamente transforma-la em uma região do tipo I. ! Para descobrir como vamos fazer isso... Bem, continua comigo aqui na linha rsrs.
Passo 3
Ok, o importante é que com essas duas informações de desigualdades conseguimos definir equações importantes:
Agora estamos preparados para desenhar a região e a boa notícia é que para fazer isso, basta colocar essas quatro equações em forma de curvas no plano , Veja:
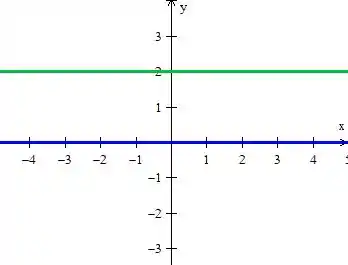
- A primeira equação, , nos representa uma reta paralela ao eixo e que passa justamente por . (Reta azul)
- A segunda é parecida com essa primeira, mas passa por . (Reta verde)
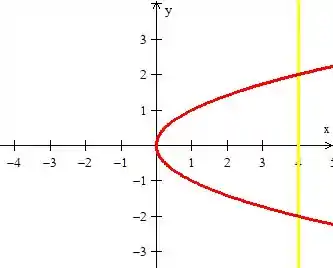
- Quanto à terceira curva, , ela nos representa a reta amarela.
- A quarta, não se preocupe, é apenas o gráfico de uma parábola inversa (ao redor de ):
Juntando as curvas em um único gráfico (você já pode ir desenhando elas no mesmo gráfico) conseguiremos entre elas a região que estamos trabalhando entre elas :D
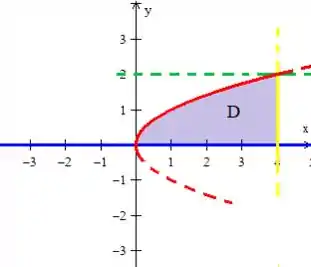
Região encontrada... Basta que troquemos e a descrevemos do outro tipo como havíamos comentado: Região do Tipo I...
Passo 4
Nessa configuração de Região, devemos pegar o variando em um intervalo numérico.
Mas espera um minuto! Ele está variando de onde até a onde?
Bem, repare então que precisamos definir qual é aquele ponto de intersecção entre a reta azul e a curva vermelha (que aparentemente nos parece muito à origem):
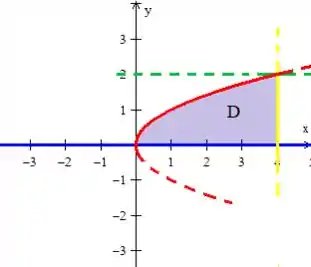
Fazer isso é bem simples, basta substituir o na parábola:
Então agora podemos falar sem dúvidas que o varia de até o que é a reta amarela:
Passo 5
Enquanto isso, o precisa variar de uma base até a um teto:
A base é a reta azul (), enquanto o teto é a parte positiva da parábola...
Passo 6
O que nos falta agora é basicamente voltar para a integral dupla e substituir essa nova descrição que encontramos:
Montando a integral lembrando que o limite numérico sempre vem primeiro, ganhamos:
Agora sim, vamos ver se dar para integrar???
Passo 7
Integrando a parte de dentro...
Veja que a função só é uma função de e agora estamos integrando em , logo...
Olha que legal!!! Agora deu para integrar, saca? =) ...
Prontinho! Conseguimos, trocando a ordem, resolver o que parecia ser impossível !