Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
(3) Encontre os limites de integração para a variável após a mudança de ordem de integração na integral
Passo 1
Pois bem! Em problemas como esse, troca de ordem de integração, devemos sempre começar fazendo um esboço da região.
Para fazermos isso, você terá que retirar da integral, duas informações maravilhosas que são o intervalo de (que no caso é o intervalo de fora):
e o intervalo de :
OBS. IMPORTANTE: Pow! Repare que com o variando em um intervalo numérico bem definido e o entre funções nos configura uma região do tipo I e o que devemos fazer é basicamente transforma-la em uma região do tipo II. !
Passo 2
Com essas duas informações de desigualdades conseguimos definir equações importantes:
Agora estamos preparados para desenhar a região e a boa notícia é que para fazer isso, basta colocar essas quatro equações em forma de curvas no plano , Veja:
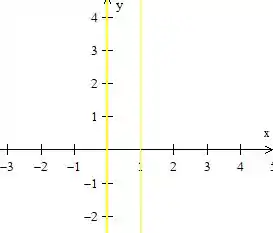
Colocando e no plano, obtemos:
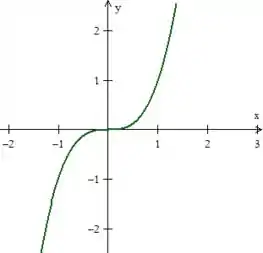
Quanto à terceira curva, , ela nos representa essa curva típica de funções cúbicas aqui, oh:
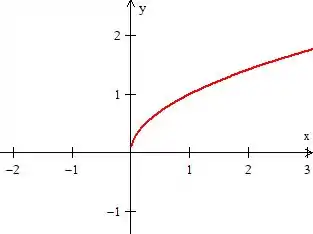
A quarta é o gráfico de
Formando então esse Região aí no interior das curvas:
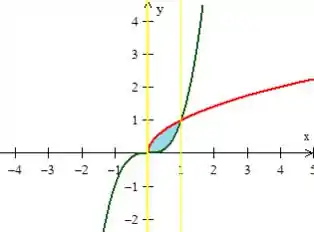
Atenção que é muito comum não sabermos se a curva da raiz está por cima ou por baixo da cúbica, mas o bizu é sempre olhar para o intervalo de onde as tirou
Como está por baixo aí, na sua região o pedacinho dele também estará!
Passo 3
Região encontrada... Basta que troquemos e a descrevemos do outro tipo como havíamos comentado: Região do Tipo II. Então venha comigo! :D
O , como região do tipo , precisa variar de uma curva até a outra.
Repare que conforme o aumenta, ele entra primeiro na região na curva da raiz (curva vermelha)
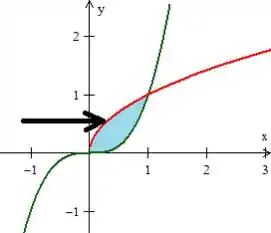
e sai na curva da cúbica em verde
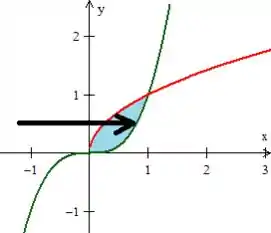
Logo
A curva vermelha tem equação , ou, isolando o , .
A curva verde é ... Ou, . Logo